Secure Computer Systems
Distributed Systems Basics
11 minute read
Notice a tyop typo? Please submit an issue or open a PR.
Distributed Systems Basics
With distributed systems we might have a server communicating with a user over an open network. An adversary might see this traffic and could maybe modify it.
What's Different in Distributed Systems?
The user/principal is on the client host and is communicating on an open network with the service host. The service host has protected resources that are protected by the TCB.
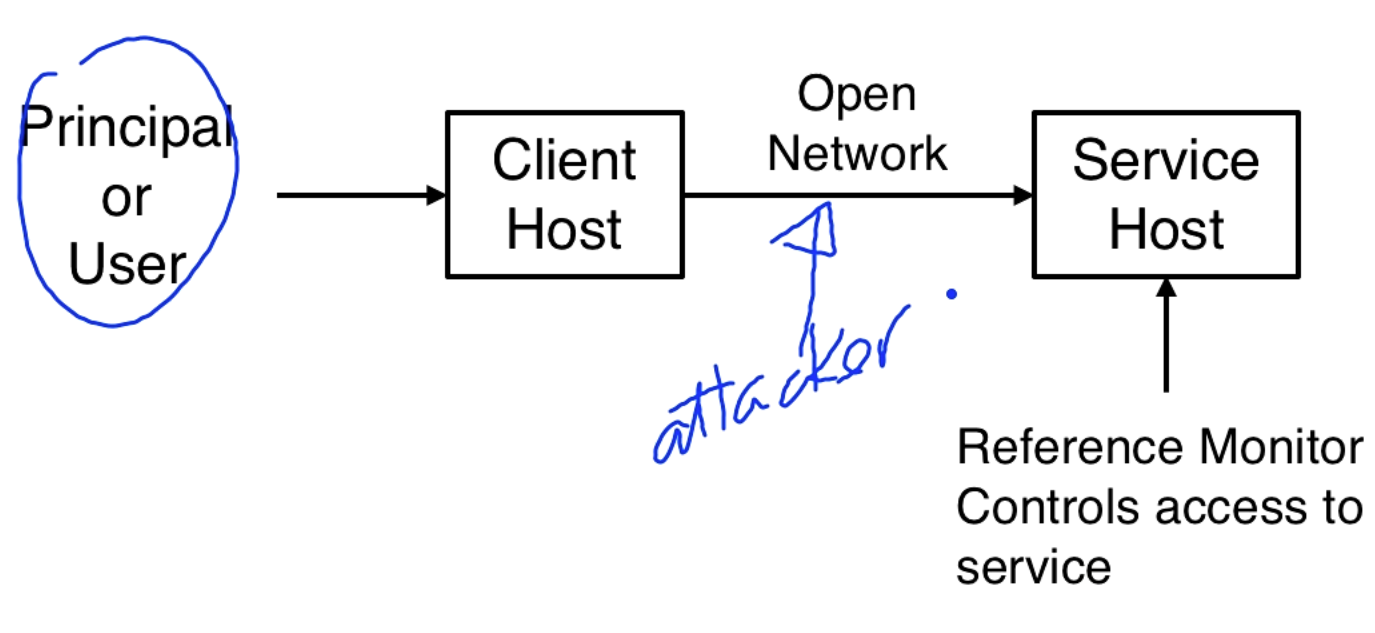
Principals make requests to perform operations on objects that reside on remote hosts. The reference monitor on the remote host makes deny/grant decisions. The reference monitor needs to know who is making the request and authorize this request with an access control policy.
Key challenges:
- Authentication when a direct trusted path does not exist between user and TCB.
- Authorization when requests come over the network and someone else (like a network channel) has to make the request on behalf of the user.
- Access control policy enforcement might be defined across different entities.
Handling Requests
A user does not directly request a resource R from the TCB on the server machine. Instead of directly making the request, the request comes through a communication channel.
The access control policy says who has access to a resource. In the distributed setting the person making the request doesn't have to be the person named in the policy. As long as the principal making the request can be trusted at least as much as some principal having access to R, they will get access granted.
Communication channels are the principals that directly deliver requests to the server. These channels are things like network connections, system calls, and decryption of encrypted messages. With encrypted communications, keys can be principals.
We look at both the theory and practice of authentication and authorization in distributed systems.
- Theory gives us a language for making precise statements about security actions
- Practice addresses actual protocols and their implementation
- Security analysis convinces us if the system is secure against certain threats
Example: Entities Involved in a Request
A user might be using an accounting app that needs to read a file from a file service on a server, below is a diagram.
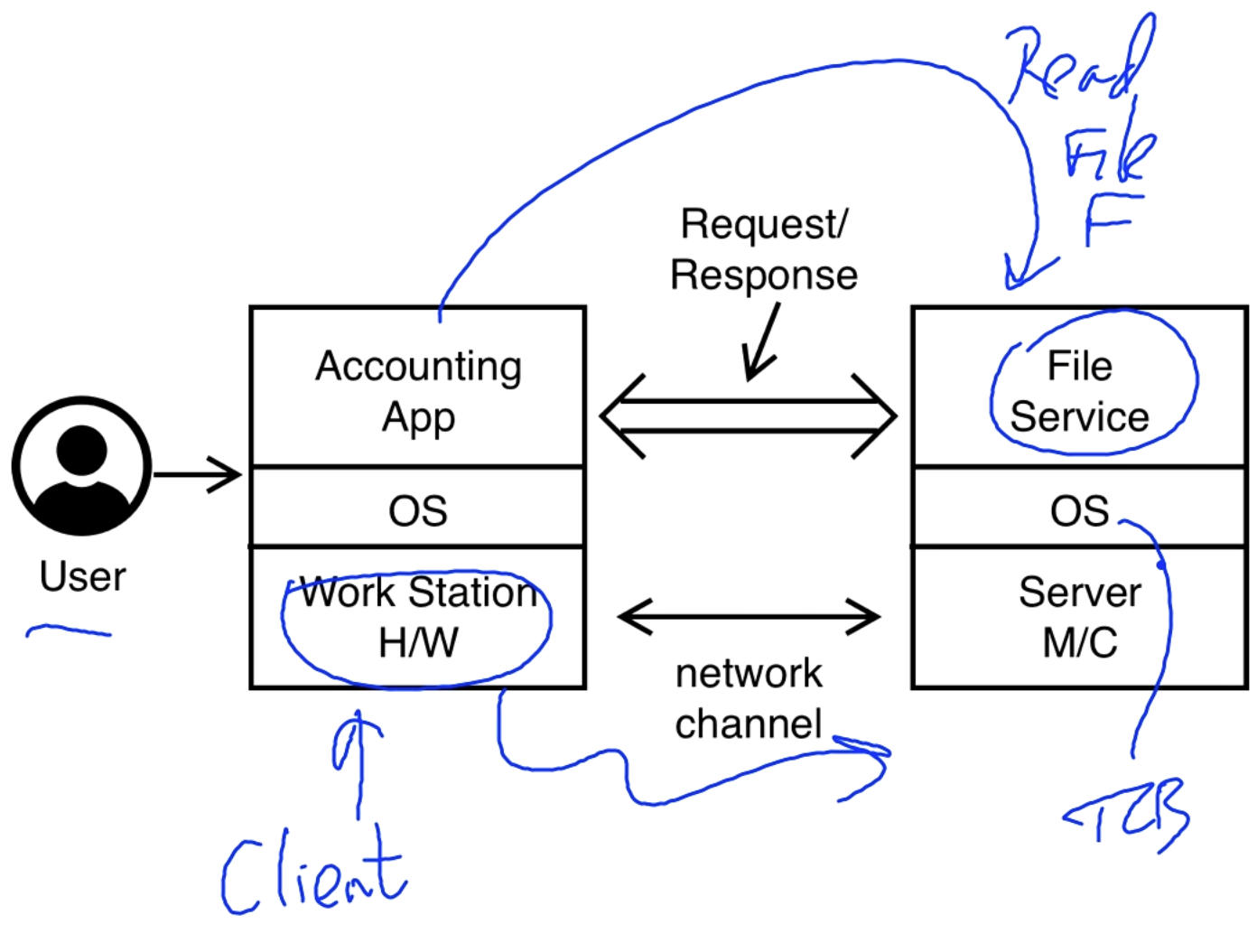
Questions
Here are some relevant questions from the server's perspective:
- Who is the requesting user?
- Is the application legitimate or is it compromised? Is it a trojan?
- Can we trust the OS?
- Is the hardware who it claims to be?
- Is the communication channel secure?
from the client's perspective:
- Is the server who it claims to be?
- Can the server OS be trusted?
- Can the server's file system be trusted?
Assumptions
- We assume the hardware and local OS, when booted securely, are trusted.
- Encrypted channels are secure and trusted.
We precisely state these assumptions when discussing theory. These assumptions lead to a system with some security properties. Are we happy with the resulting security?
Note: Other than the stated assumptions, we need to build everything else in a demonstrably trusted manner.
Principals and Statements
Principals can be either simple or compound
-
Simple principals can be represented as just a name string. This string can represent many different things.
- People, machines, roles and groups (sets of principals)
- Channels (network IP addresses, I/O ports, wires)
- Encryption keys
-
Compound principals are made from combining simple principals. There are three operations: as, and, for.
- Principals in Roles: Abadi as Manager
- Conjunction: Abadi and Burrows
- Delegation: Abadi for Burrows
Principals make statements to request access, grant access, or to define policy. In a distributed system all requests happen over channels, so channels are the only principals able to directly make a request.
The speaks for operator allows one principal to speak for another principal. In particular the channel speaks for a user, making a statement. Authentication lets us answer the question of who is making a statement.
There are primitive statements like "read file F". Primitive statements can be combined using operators, let and be statements:
- is implies
- is and
- is equals
We can also combine principals, if and are principals then (A speaks for B) is a statement.
Statements define a language. Requests, policies, and all security relevant actions are made in this language. The operators for statements are as given here. In particular, there is no not symbol. not causes problems.
What Statements are Valid?
I'm going through this rather quickly, you might want to read the sections in the paper a couple of times - Dr. Mustaque Ahamad
Some statements are true by definition. We call these axioms. To say that a statement is true, we put double quotes before it. .
If is an axiom, because we assume the truth of the axiom. There are things called theorems that can be proven from axioms. If is a theorem because it follows from the axioms.
If and then . This is saying if a thing is true and it implies another thing then the other thing is true, and we call it modus ponens.
-
If a statement is true it doesn't matter who says it, it is true that the person says it.
- then says for every principle .
-
(A says s and (A says s s')) s'
- The above statement is true because it is like "if A and (A implies B) then B". Modus ponens.
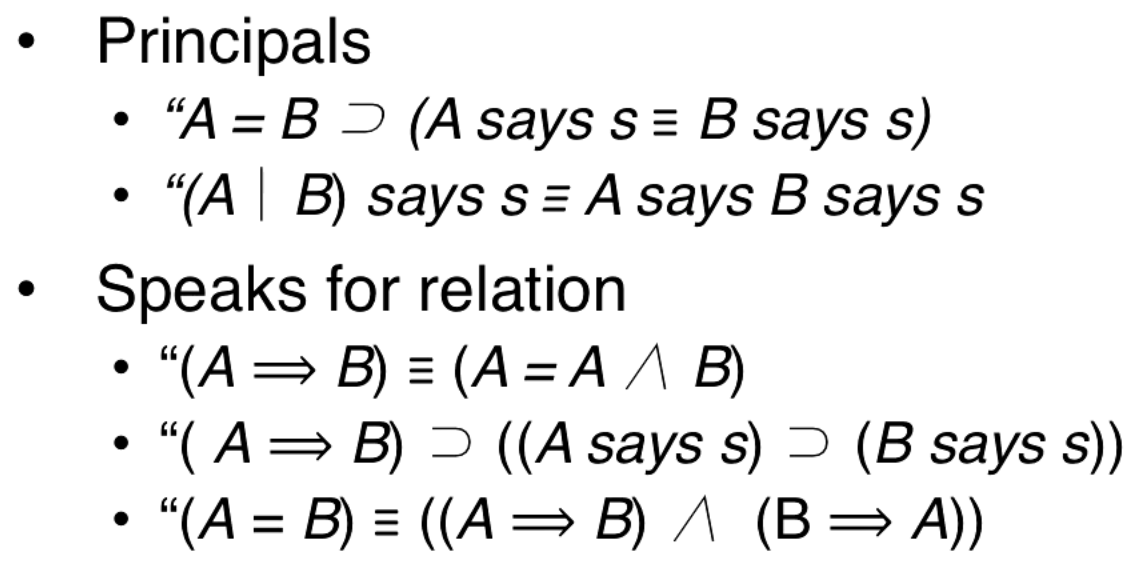
Principals
- If A and B are the same principle, then anything that A says is equivalent to B saying it.
-
(A quotes B says s) is equivalent to (A says B says s)
- The | operator is the "quotes" operator.
Speaks for relation
- (A speaks for B) is equivalent to (A equals (A and B))
- (A speaks for B) implies (if A says s then B says s)
- (A and B are equal) is equivalent to (A speaks for B and B speaks for A)
Granting Requests: An Example
Statements 1 and 2 are requests that are being made to read a file. Statements 3, 5, and 7 are statements about the policy, policy statements must be made by someone trusted. Statements 4 and 6 are statements about certification, certificate authorities are trusted entities and we discuss them more later.
Remember that means " speaks for ".

This next picture is confusing, I'll try to explain after you look at it.
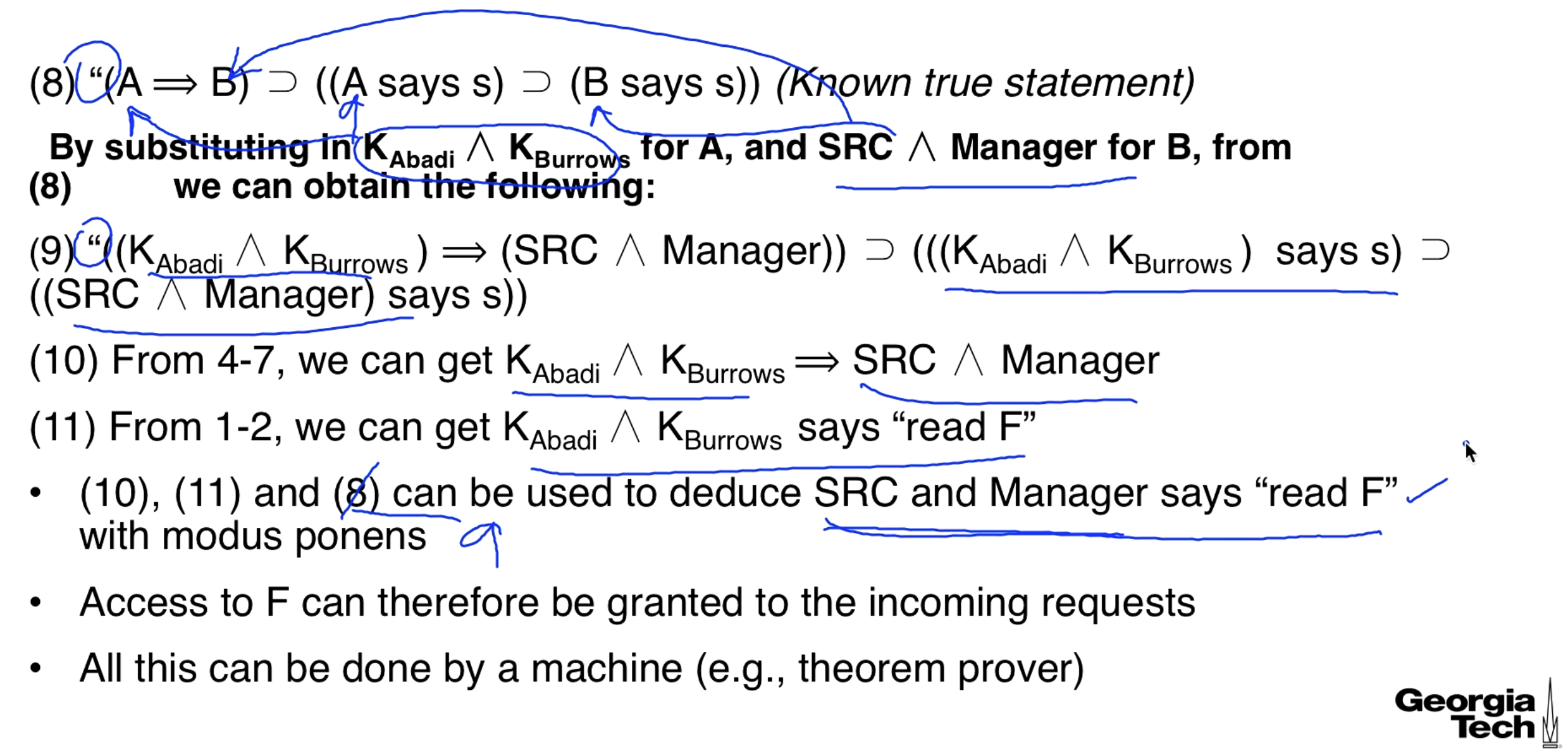
We have keys that say stuff but we need to have SRC and Manager saying it.
The "speaks for" operator is transitive so this can be simplified to
In the paper and in the lecture they make this next step by saying it follows from monotonicity. Not very rigorous, but maybe the proof is obvious (not to me).
That is how we get step 10. Step 11 is more self-explanatory. And the whole point is that is true, so what it implies is true, which is another implication, which ends up implying that SRC Manager says to read the file.
Securing Communication Channels
In distributed systems there is a network we have to communicate over.
- We have a logic to define statements and check the validity of these statements.
- Principals can make simple or compound statements.
-
We don't directly talk to remote nodes, only channels can make statements directly.
- A channel C speaks for some other principal and makes statements on its behalf.
- The network is open and implements a communication channel across nodes.
-
Threat model
- Passive: observe communication over the network
- Active: alter or inject communication (man in the middle)
Securing the Open Network
For a communication channel to be secure we must have the following:
- C is confidential: You can't read messages over the channel unless you are allowed.
- C has integrity: We know who can send messages to C.
To authenticate C we must find the principal A such that C A (C speaks for A). We can do this by having A or someone who speaks for A say "A says C A".
Hand-off Axiom: If (A says (C A)), then C A.
An example might look something like:
From this it is true that . This works because . Then we substitute Bob in for to get Bob says (C Bob), which from the hand-off axiom makes it so that C Bob. '
Encryption
We encrypt a statement S with K. This results in K says S. We decrypt with to get S. In public key cryptography K is a public key and is a private key. In shared key cryptography =
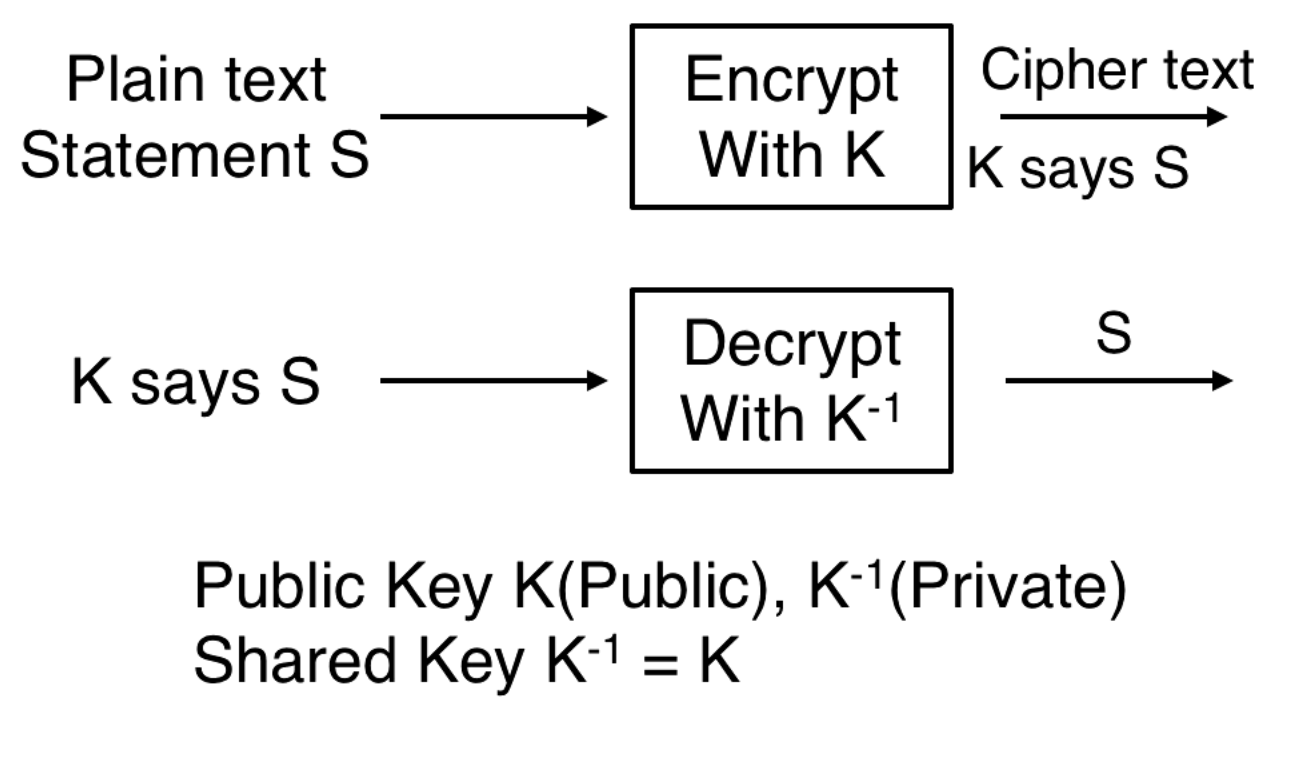
Sharing Keys
Constructing Practical Secure Channels
- We have a key and key identifier . r is an identifier for the key K that tells you which key to use to decrypt K.
- are identifiers for K which is shared by principals A and B.
- How do we generate ? How do we generate ?
-
How do we share and ?
- could be an index into a key table or where is R's master key.
Node to Node
We must generate a key K and share it with A and B. Messages are sent from A to B, the message includes B's identifier for K so that B knows what key to use. The keys are shared with a key exchange protocol.

Diffie-Hellman Key Exchange
Exchanging Keys
The protocol is for setting up a authenticated secret channel between two parties. For the authentication, we assume each endpoint has a public/private key pair. With this assumption, each party can generate a random key, send it to the other by encrypting with its public key and then use the two random keys (one it generates and one it receives from the other party) to generate the channel key. There are few other details like key identifiers etc. which are needed to implement it. - Prof. Mustaque
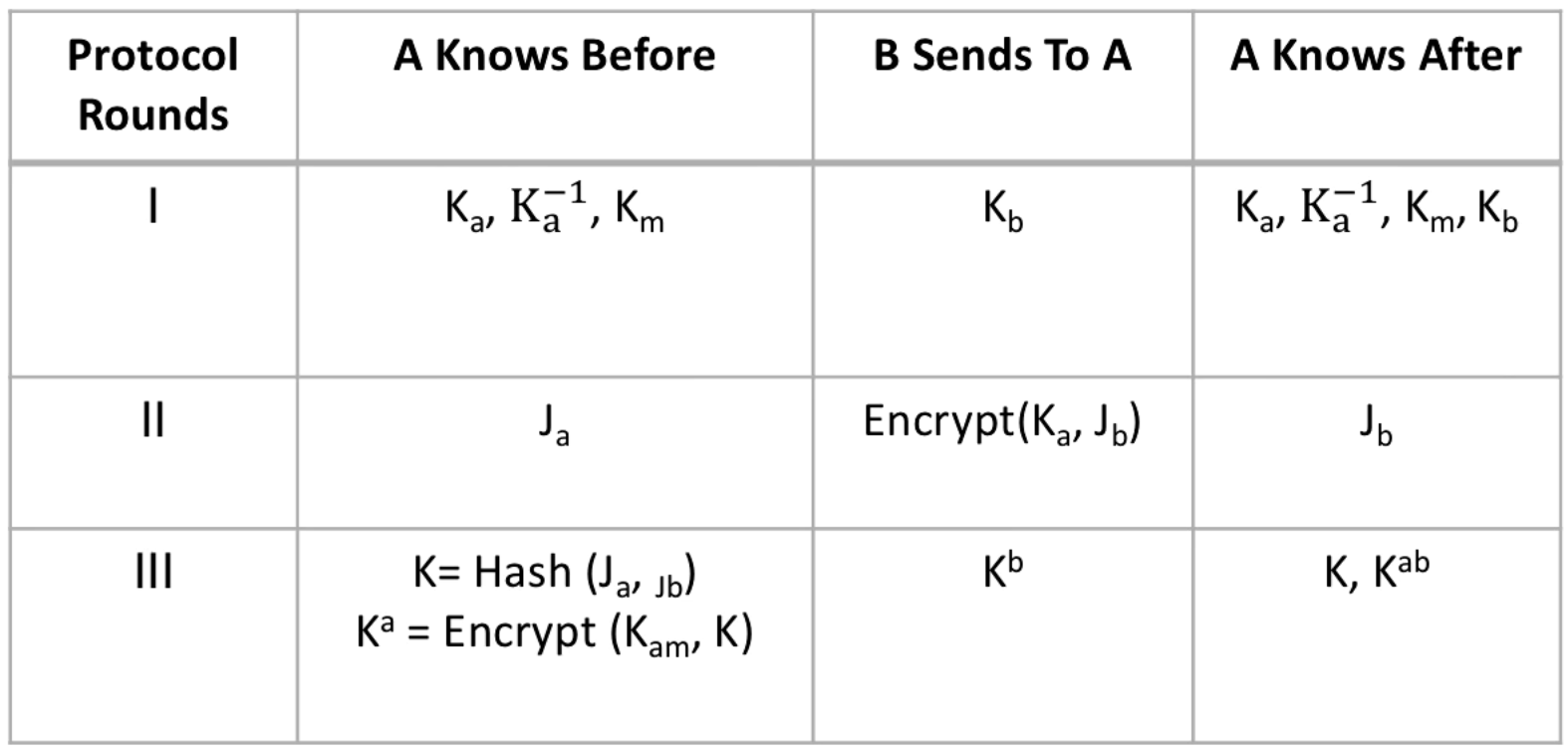
I don't recognize this as Diffie-Hellman, in Diffie-Hellman we would combine with to get our shared key? If you can clarify please submit a PR.
Secure Messages from A to B
We want the statement A says s, but we have to say this securely. This is why we did the key exchange so that the following is true -
- K says s (B receives a message from the shared K created in key exchange)
- K
Since K speaks for and speaks for A, we know that K speaks for A. B knows it did not send the message and therefore A sent the message because K can speak for A and B.
Named Principals and Certificates
We need a trusted entity that can define relationships between keys and users, like associating with the user Abadi. This trusted entity is called the certificate authority (CA). To say that the CA is trusted is to say that .

The CA issues statements about what keys speak for who and signs them with its private key. These statements are verified by users using the public key of the CA.
Certificate Revocation
CAs are mostly offline. The CA's private key signs all the statements about what keys speak for who. This makes the CA an attractive target for hackers that would like to sign statements as the CA. We can minimize the risk to the CA by minimizing it's connectivity (i.e. it is offline).
Certificates can be revokes for a number of reasons, like if a user's private key gets leaked or if there is an expiration date.
We can keep the CA offline and have an online agent that tracks which certificates are revoked. When we get a statement signed by a CA we can check if the certificate has been revoked.
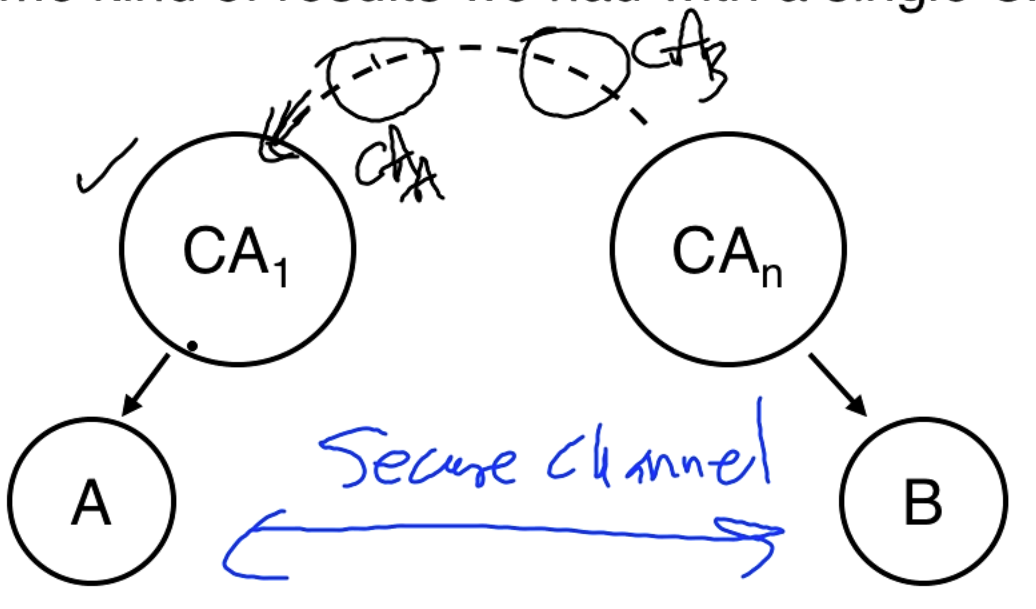
Distributed Trust
A single CA for the entire internet is problematic. We can have hierarchical CAs. So is the root CA of B. A trusts but not which signs the certificate of B. So is used in a chain of trust that goes down to B and will end up signing the statement that is sent to A. The details are discussed in the paper but this is the depth discussed in the lecture.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy