Databases
SQL
14 minute read
Notice a tyop typo? Please submit an issue or open a PR.
SQL
SQL Introduction
SQL is the lingua franca of databases, or as Mike Stonebraker called it, the intergalactic data speak. Most databases support some form of SQL, and most data sit in relational databases accessed through SQL. Although we use XML frequently to describe interfaces and exchange data, the vast majority of data still sits in the SQL databases.
SQL History
SEQUEL, or Structured English QUEry Language, was the original name for SQL. SEQUEL - created by Donald Chamberlin and Raymond Boyce - was part of a research relational database prototype released by IBM in 1973 called System R. SEQUEL was later changed to SQL, or Structured Query Language. SQL is based on relational tuple calculus primarily with some foundation in relational algebra.
There are both ANSI and ISO standards for SQL. The first version of SQL was standardized in 1986, with a revision in 1989. SQL2 came later in 1992, and SQL3 was published in 1999. There have been several revisions since the release of SQL3: in 2003, 2006, 2008, and 2011, for example. Most revisions did not change the core SQL standard but added new functionality for features like temporal and spatial queries, among others.
Many database products implement the SQL standard completely or partially, including IBM Db2 (a commercial version of SYSTEM R), Oracle, Sybase, SQLServer, MySQL, and many more.
Insert
Let's look at an example of insertion. The following statement inserts a tuple
into UserInterests that has a value of 'user12@gt.edu' for Email, 'Reading'
for Interest, and 5 for SinceAge:
INSERT INTO UserInterests(Email, Interest, SinceAge)
VALUES ('user12@gt.edu', 'Reading', 5)This method of insertion only adds a single row at a time into the database. We can augment an insertion statement with a query selection on the database to insert the result of such a selection - zero or more tuples - into a table.
Delete
Let's see an example of a delete operation. Whereas the insertion statement we
saw earlier only inserts one tuple into the table, deletion can delete a set of
rows in the table. The following query deletes all tuples from UserInterests
where Interest is 'Swimming':
DELETE FROM UserInterests
WHERE Interest = 'Swimming';Update
Let's look at an update. Similar to deletions, update operations may impact a
set of tuples. The following statement sets the Interest to 'Rock Music' for
every tuple in UserInterests where Email is 'user3@gt.edu' and Interest is
'Music':
UPDATE UserInterests
SET Interest = 'Rock Music'
WHERE Email = 'user3@gt.edu'
AND Interest = 'Music';General SQL Query Syntax
Generally, we select a list of columns from a collection of tables where some condition evaluates to true. With a few exceptions, all SQL queries take the following shape:
SELECT column_1, column_2, ..., column_n
FROM table_1, table_2, ..., table_m
WHERE condition;The columns above refer to the names of database columns, such as BirthYear,
in our database tables. The tables refer to names of database tables, such as
RegularUser. The condition consists of comparisons between columns and either
constants or other columns. For example we might look for rows where `BirthYear
1985
orCurrentCity = HomeTown`. We combine conditions using nesting, conjunction, disjunction, or negation, just as we did in relational calculus and algebra.
When discussing commercial relational databases, as opposed to algebra and calculus, we use the terms column, table, and row, instead of attribute, relation, and tuple, respectively. The SQL query shown above is equivalent to the following algebra expression:
In the expression above, we take the Cartesian product of the relations of
interest. Then we select the tuples that evaluate to true for our expression.
Finally, we project the result onto the attributes of interest. We can remove
the selection operation from the algebra expression if the SQL query has no
WHERE clause.
Selection - Wildcard
The following query selects all rows from the RegularUser table:
SELECT Email, BirthYear, Sex, CurrentCity, HomeTown
FROM RegularUser;Notice that there is no WHERE clause in this expression. Also, notice that we
are explicitly enumerating all columns from RegularUser. We have this
shorthand available when selecting all columns:
SELECT *
FROM RegularUser;Selection - Where Clause
The following query selects all columns for all rows from RegularUser where
HomeTown equals 'Atlanta':
SELECT *
FROM RegularUser
WHERE HomeTown = 'Atlanta';Selection - Composite Where Clause
The following query selects all columns for all rows from RegularUser where
CurrentCity equals HomeTown or HomeTown equals 'Atlanta':
SELECT *
FROM RegularUser
WHERE CurrentCity = HomeTown OR
HomeTown = 'Atlanta';Projection
Let's say we only need information from some of the columns of the RegularUser
table - namely, Email, BirthYear, and Sex - for all users who live in
Atlanta. We can express this query as such:
SELECT Email, BirthYear, Sex
FROM RegularUser
WHERE HomeTown = 'Atlanta';The resulting table has the columns specified in the query in the same order in which we enumerated them.
Distinct
When we looked at relational algebra and calculus, we emphasized that relations are sets and that the result of a query is always a relation and, therefore, a set. In SQL, tables may have duplicate rows. Suppose we want to find the sex of all regular users in Atlanta. We can express that query as:
SELECT Sex
FROM RegularUser
WHERE HomeTown = 'Atlanta'If we have multiple rows in RegularUser with the same value of Sex, we will
have duplicate rows in our resulting one-column table. We can avoid such
duplication with the DISTINCT keyword:
SELECT DISTINCT(Sex)
FROM RegularUser
WHERE HomeTown = 'Atlanta';Natural Inner Join - Dot Notation
Suppose we want to find the email, birth year, and salary for regular users who
have a salary by joining the RegularUser table and the YearSalary table, the
latter of which has BirthYear and Salary columns. The appropriate SQL query
looks as follows:
SELECT Email, RegularUser.BirthYear, Salary
FROM RegularUser, YearSalary
WHERE RegularUser.BirthYear = YearSalary.BirthYear;Notice that our result does not have information about the last four users as
their birth year is not present in YearSalary.

When there is no ambiguity about which columns come from which tables, as is the
case for Email and Salary above, we can reference the columns without
specifying the table. Since BirthYear appears in both tables, we use dot
notation to clarify which column we are referencing. RegularUser.BirthYear
is not ambiguous, whereas BirthYear is.
In relational algebra, we didn't have to specify the join condition when the
attribute names were the same. In SQL, we must specify this condition:
RegularUser.BirthYear = YearSalary.BirthYear. However, when the column names
are the same, we also have an alternative syntax available to us:
SELECT Email, RegularUser.BirthYear, Salary
FROM RegularUser NATURAL JOIN YearSalary;If constituent tables share no columns of the same name, the natural join operation defaults to the Cartesian product.
Natural Inner Join - Aliases
As before, suppose we want to find the email, birth year, and salary for regular
users who have a salary by joining the RegularUser table and the YearSalary
table, the latter of which has BirthYear and Salary columns. We can use
aliases to rewrite this query as follows:
SELECT Email, R.BirthYear, Salary
FROM RegularUser AS R, YearSalary AS Y
WHERE R.BirthYear = Y.BirthYear;When we discussed tuple calculus, we encountered the concept of tuple variables;
R and Y are exactly tuple variables. For the scope of this query, we alias
the RegularUser and YearSalary tables as R and Y, respectively, and we
can reference these tables using their aliases anywhere in the query. When we
use R or S to range over RegularUser or YearSalary, we can imagine the
alias taking on the value of each row of the corresponding table in turn during
the query evaluation.
SQL queries can become quite large and complex, and we can use aliases to save on typing. We also use aliases to disambiguate table references; in particular, we must use aliases when joining a table with itself to distinguish between the first and second instances of the table in the join.
Left Outer Join
Suppose we want to find the email, birth year, and salary for regular users who
have a salary by joining the RegularUser table and the YearSalary table. We
also want to include regular users who have no salary in the result. We can
express this query as follows:
SELECT Email, RegularUser.BirthYear, Salary
FROM RegularUser LEFT OUTER JOIN YearSalary;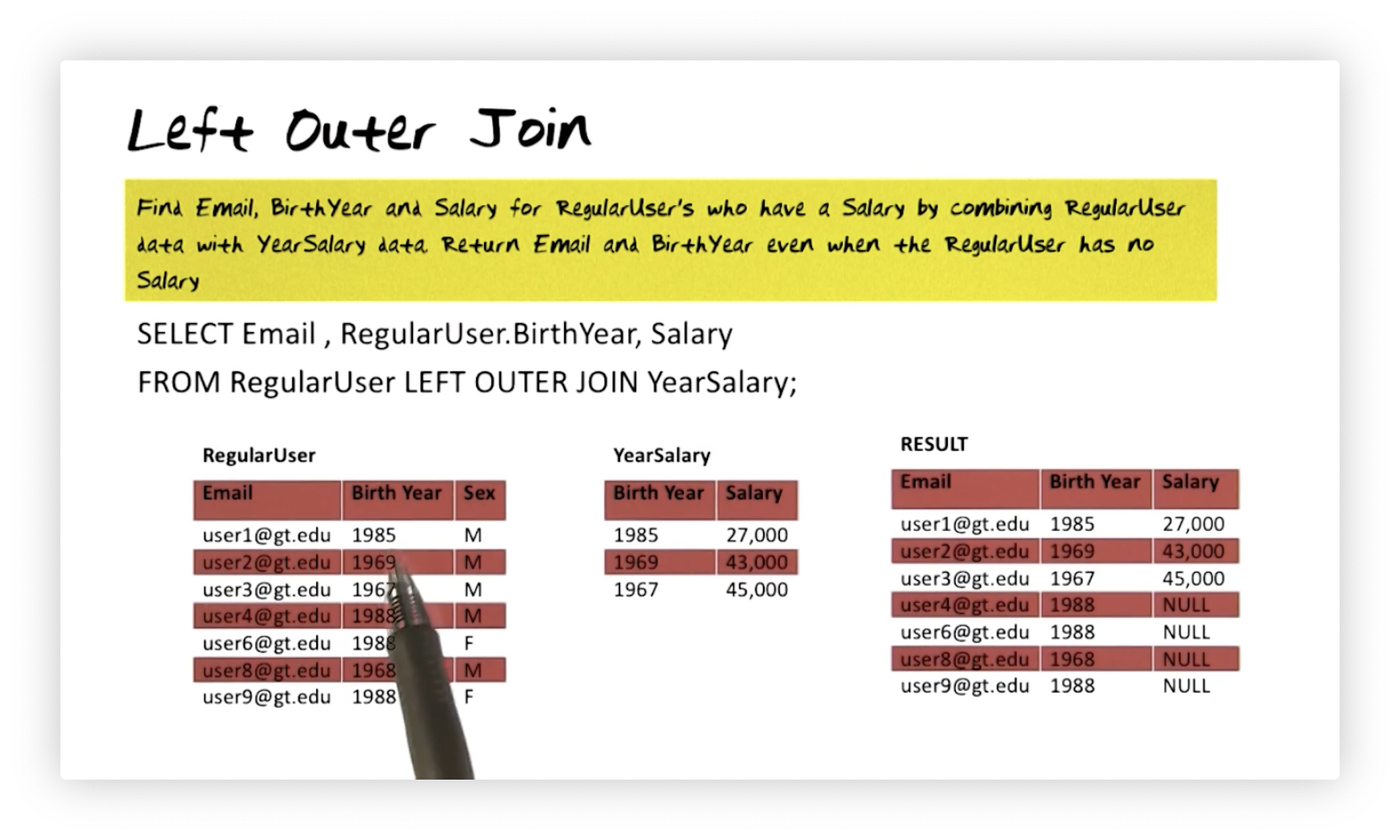
In this example, users who do not have associated salary information are
included in the result but have NULL values for the Salary column in the
resulting table.
String Matching
Until now, most of the SQL queries we have looked at have been SQL versions of
relational algebra queries (except DISTINCT). However, SQL databases are
practical tools and, therefore, must have capabilities outside the scope of
abstract relational algebra and calculus.
The second practical operation we examine is string matching. Suppose we want to find information about regular users who currently live in a city that starts with "San". We can express that query as such:
SELECT Email, Sex, CurrentCity
FROM RegularUser
WHERE CurrentCity LIKE 'San%';The percent sign, '%', above matches any string, including the empty string. For example, 'San%' matches the literal string 'San' and 'San' plus any number of subsequent characters. Let's look at the result, which includes regular users living in San Diego and San Francisco.

There are more types of wildcards in string matching. Whereas '%' matches zero or more characters, the '_' character matches exactly one character. For example, we can select regular users who currently live in cities that have precisely six characters where the first letter is "A" with this query:
SELECT Email, Sex, CurrentCity
FROM RegularUser
WHERE CurrentCity LIKE 'A_____';Using the image above, we can see that the result of this query will only include the regular user who currently lives in Austin.
Sorting
Sorting is another practical concern that does not have roots in algebra or calculus. Suppose we want to find data about regular male users and need that information sorted by current city. We can express that query as follows:
SELECT Email, Sex, CurrentCity
FROM RegularUser
WHERE Sex='M'
ORDER BY CurrentCity ASC;
It is possible to sort on multiple columns, and we can specify the sort
direction as ascending, ASC, or descending, DESC, for each column we sort.
Set Operations - Union
Suppose we want to find all current cities and hometowns (without duplicates)
from the RegularUser table. We form two queries - one that selects all current
cities and one that selects all home towns - and then we find their set union
using the UNION operator:
SELECT CurrentCity
FROM RegularUser
UNION
SELECT HomeTown
FROM RegularUser;Whereas SQL queries generally may return duplicates, the union, intersection,
and set difference operators only return sets. If we want duplicates in our
result, we would instead reach for the UNION ALL operator:
SELECT CurrentCity
FROM RegularUser
UNION ALL
SELECT HomeTown
FROM RegularUser;
Set Operations - Intersection
Suppose we want to find all cities that are someone's current city and
someone's hometown without including any duplicates. We form two queries - one
that selects all current cities and one that selects all home towns - and then
we find their set intersection using the INTERSECT operator:
SELECT CurrentCity
FROM RegularUser
INTERSECT
SELECT HomeTown
FROM RegularUser;As we saw with the UNION operator, the INTERSECT operator removes duplicates
from the resulting table. If we want duplicates in our result, we would instead
reach for the INTERSECT ALL operator:
SELECT CurrentCity
FROM RegularUser
INTERSECT ALL
SELECT HomeTown
FROM RegularUser;
Set Operations - Except
Suppose we want to find all cities that are someone's current city but not
someone's hometown without including duplicates. We form two queries - one that
selects all current cities and one that selects all home towns - and then we
find their set difference using the EXCEPT operator:
SELECT CurrentCity
FROM RegularUser
EXCEPT
SELECT HomeTown
FROM RegularUser;As we saw with the UNION and INTERSECT operators, the EXCEPT operator
removes duplicates from the resulting table. If we want duplicates in our
result, we would instead reach for the EXCEPT ALL operator:
SELECT CurrentCity
FROM RegularUser
EXCEPT ALL
SELECT HomeTown
FROM RegularUser;
San Diego appears as a current city twice in RegularUser and a hometown once.
Notice that this city appears in the result of the query using EXCEPT ALL but
not the one using EXCEPT. Why? If we subtract a multiset with one occurrence
of a value from a multiset with two occurrences of a value, we end up with a
multiset with one occurrence of the value.
Built-in Functions
Continuing our discussion about practical functionality in commercial databases,
let's consider some built-in functions, such as count, sum, avg, min,
and max.
Suppose we want to count the number of regular users. We can use the count
built-in to retrieve the number of rows in RegularUser:
SELECT count(*)
FROM RegularUser;Suppose we want to select the email and birth year for the youngest female
regular user. Since the youngest users have the "largest" birth years, we can
use the max built-in like so:
SELECT Email, max(BirthYear)
FROM RegularUser
WHERE Sex = 'F';
Group By
Sometimes, we want to group the data that comes back from a query and apply some simple calculations within each group. For example, suppose we wish to group user interests by user email. For each group, we want to return the corresponding email, the number of interests the user has, and the user's average "since age". Furthermore, we want to sort the result by the number of interests ascending. Here's that query:
SELECT Email, count(*) AS NumInt, avg(SinceAge) AvgAge
FROM UserInterests
GROUP BY Email
ORDER BY NumInt ASC;
Having - Condition on the Group
Suppose we want to group user interests by user email. For each group, we want
to return the corresponding email, the number of interests the user has, and the
user's average "since age". Furthermore, we want to sort the result by the
number of interests ascending. This time, we want only to return the groups with
more than one interest. We can accomplish this with a HAVING clause:
SELECT Email, count(*) AS NumInt, avg(SinceAge) AvgAge
FROM UserInterests
GROUP BY Email
HAVING NumInt > 1
ORDER BY NumInt ASC;
Notice that user four is absent from this query since they only have one interest.
Nested Queries - IN/NOT IN
The final SQL concept we will explore is nested queries. Let's start by retrieving the email and interests of all regular users in Atlanta.
SELECT Email, Interest
FROM UserInterests
WHERE Email IN (
SELECT Email
FROM RegularUser
WHERE HomeTown = 'Atlanta'
);
We can envision this query in two ways. We can start with UserInterests and
see if the email for each row is associated with a regular user who lives in
Atlanta. Alternatively, we can start with RegularUser, retrieve the email of
all users in Atlanta, and then find the interests for those emails from
UserInterests. We say there is no correlation between the tuples considered in
the outer and inner queries; in other words, the inner query returns the same
result regardless of the outer query.
An alternative way to express this query without nested queries is by joining
UserInterests on RegularUser and selecting the appropriate rows:
SELECT U.Email, Interest
FROM UserInterests I, RegularUser U
WHERE I.Email = U.Email AND
HomeTown = 'Atlanta';Nested Queries - Comparisons, SOME/ALL
Let's find current cities with at least one regular user with a salary higher than all salaries of regular users from Austin.
SELECT CurrentCity
FROM RegularUser R, YearSalary Y
WHERE R.BirthYear = Y.BirthYear AND Salary > ALL
(SELECT Salary
FROM RegularUser R, YearSalary Y
WHERE R.BirthYear = Y.BirthYear AND HomeTown = 'Austin'
)
Let's focus on the inner query first. Since the Salary and HomeTown columns
are not in the same table, we must first join YearSalary and RegularUser.
Next, we select the rows where HomeTown is Austin and the birth years are
equal. Finally, we project the result of the join and selection onto Salary,
leaving us with the salaries from regular users who live in Austin.
Let's now turn to the outer query. Again, we must join YearSalary and
RegularUser since we need both CurrentCity and Salary information. Which
rows do we select? We only want the rows where the birth years are equal, and
the Salary is greater than all the values of the inner query - namely, the
salaries of individuals from Austin. Finally, we project that selection onto
CurrentCity, and we have our final answer.
Notice that we don't actually need to ensure that each considered salary is greater than all the salaries of users from Austin; we only need to ensure that it's greater than the maximum of those salaries. Consider this alternative query:
SELECT CurrentCity
FROM RegularUser R, YearSalary Y
WHERE R.BirthYear = Y.BirthYear AND Salary >
(SELECT max(Salary)
FROM RegularUser R, YearSalary Y
WHERE R.BirthYear = Y.BirthYear AND HomeTown = 'Austin'
)Nested Queries - Correlated
The last type of nested query we will examine is correlated queries. Suppose we want to find the email and birth year of regular users who have no interests:
SELECT R.Email, BirthYear
FROM RegularUser R
WHERE NOT EXIST
(SELECT *
FROM UserInterests U
WHERE U.Email = R.Email)
In the inner query, we select everything from UserInterests where the email
associated with the interest equals the email of the regular user row being
considered. Notice that the variable R is not defined in the inner query; this
is known as a reference out of scope. The outer query defines R, and the
inner query holds a reference to this query. As a result, we cannot evaluate the
inner query without the outer query; the two are correlated.
We can picture this inner query being evaluated once for each row in the outer
query. For example, consider the first row in RegularUser. To determine if we
can include the Email and BirthYear from that row, we must first execute the
inner query on UserInterests and determine if that user has any associated
interests. Since they do - music and blogging - that user is not included in the
result.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy