Introduction to Cryptography

Decryption

Encryption is the process of converting data into a form that is unintelligible to the unintended or unauthorized party. We call the original data plaintext, and the unintelligible data ciphertext. An authorized party can reverse this process; that is, they can decrypt the ciphertext to reveal the plaintext.

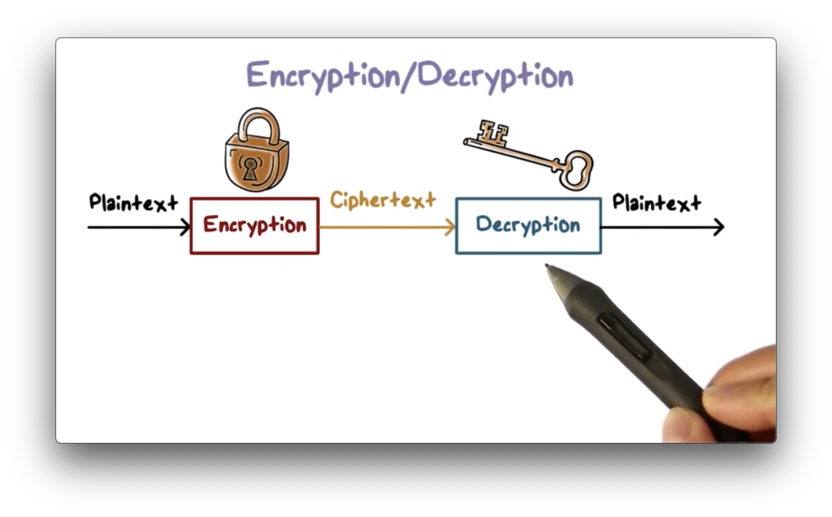
The decryption process always recovers the original plaintext because there is a one-to-one mapping between plaintext and ciphertext.

Encryption protects data confidentiality because only the authorized party with the proper secret key can read the data.

Encryption also provides other security services. We can use encryption for integrity checking to ensure that no one has tampered with a message. We can also use encryption to verify the authorship of a message. Encryption also serves as a method by which one user can authenticate themselves with another.

Encryption Basics

Encryption has been used for thousands of years. There is evidence that ancient Egyptians used ciphers - encryption schemes - and one of the most famous ciphers is the letter-based Caesar cipher from Roman times.

The ancient ciphers were all symmetric ciphers, an encryption scheme that still enjoys widespread use today. Asymmetric ciphers are much newer, only having been invented in the late 1970s.

Most modern security protocols use both types of encryption. Parties wishing to communicate typically use asymmetric ciphers to authenticate themselves with one another and to establish and exchange a symmetric encryption key. Each party encrypts and decrypts subsequent communications using this key. Senders may also use asymmetric ciphers to sign the data to prove authenticity.

Attacks on Encryption

Given that encryption plays such an essential role in security, we can expect that attackers are always trying to break our ciphers. The goal of these attackers is to recover the plaintext from the ciphertext or to uncover the encryption key.

An attacker can quickly get their hands on our ciphertext. For example, they may use a packet sniffing tool to capture encrypted packets you send over the Internet, and they might try to recover the plaintext from these packets. We should always assume that an attacker can capture the ciphertext we transmit over the Internet.

Instead of uncovering one piece of plaintext from one piece of ciphertext, the attacker may try to discover the encryption key so that they can decrypt all subsequent communications encrypted using that key. There are several attack methods to achieve this goal.

Brute-force

The simplest, most inefficient strategy is the brute-force method. In this attack, the attacker tries all possible keys one by one until they find the one that decrypts the ciphertext properly into plaintext.

How does the attacker know that the decryption has worked properly? Typically the attacker knows what the plaintext should resemble. For example, if the plaintext is an English sentence, then only the correct key can decrypt the ciphertext into text that reads like English.

This method is very inefficient because the number of possible keys can be huge. As a result, brute-force often requires an unfeasible amount of time to be successful.

Cryptanalysis

In cryptanalysis, the attacker knows the encryption algorithm and perhaps some characteristics of the data, such as the distribution of certain letters or words. An attacker can perform a much more directed search of the keyspace with cryptanalysis as opposed to brute-force.

Implementation attacks

The attacker can also exploit implementation or systems issues. For example, researchers were able to deduce the values of certain bits in an encryption key by observing the power consumption in a cryptosystem. As a result, they were able to reduce the size of the keyspace significantly.

Social-engineering attacks

The weakest link in a security system is often the naive users who can be exploited using social engineering tricks. For example, an attacker can call an unsuspecting user and pretend to be a sysadmin who has forgotten their key.

Encryption Attack Quiz

Encryption Attack Quiz Solution

In a brute-force attack, the attacker must try all potential keys. The only way to make this task more difficult is to increase the length of the key, thus increasing the size of the keyspace.

Simple Ciphers Quiz

Simple Ciphers Quiz Solution

Since "A" maps to "D", "B" maps to "E", and so forth, we can just "rewind" each letter in the ciphertext by three to obtain the plaintext.

Simple Ciphers

Caesar's cipher - an example of a shift cipher - maps each letter to another letter by shifting it a fixed amount. If we represent each letter in the alphabet as a number - A = 1, B = 2, … , Z = 26 - then we can represent this encryption scheme for a given letter and a given shift as

(letter + shift) mod 26

The secret key in this scheme is the value of shift. Since there are only 26 possible keys (any shift higher than 26 wraps back around), an attacker only needs to try at most 26 keys before being able to decrypt any message encrypted with Caesar's cipher.

A generalization of this scheme allows arbitrary mapping of one letter to another; that is, this scheme no longer requires shifting each plaintext letter by the same fixed amount. These generalized ciphers are referred to as substitution ciphers or monoalphabetic ciphers.

The substitution alphabet is the secret key in this scheme. The number of possible alphabets is vast. If I wanted to create such an alphabet, I would have 26 options for mapping "A", 25 options for mapping "B", and so forth. Put another way, there are 26! (2^88) possible alphabets. An attacker cannot brute-force this scheme.

Instead of attempting to try every key, an attacker can analyze the statistical frequency of letters in the ciphertext. For example, in English, the most frequently used letter is "E". If the most common letter in the ciphertext is "X", then there is a high probability that "E" maps to "X".

An attacker can use statistical analysis to decrypt the message directly or at least drastically reduce the size of the keyspace over which they subsequently run a brute-force attack.

Letter Frequency of Ciphers

Here is the frequency distribution of English letters.

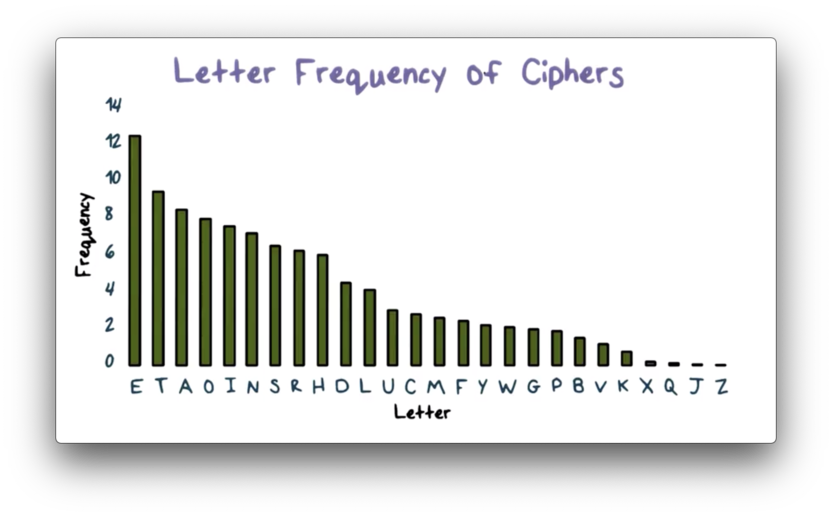
Using this frequency distribution, we should be able to make some educated guesses to decipher the following ciphertext:

IQ IFCC VQQR FB RDQ VFLLCQ NA RDQ
CFJWHWZ HR BNNB HCC HWWHBSQVQBRE
HWQ VHLQ

To start, we notice that the letter "Q" is the most frequent in our ciphertext. In English, the most common letter is "E", so there is a high probability that "Q" is the plaintext letter "E".

Then we can look at the three-letter words, RDQ and HWQ, which both end in "E". It is likely that one of these words is "ARE", while the other is "THE".

We also have the word HR, which can be "AT". If so, then HWQ is "ARE" and RDQ is "THE". If "H" is "A", then the word HCC is likely "ALL".

If we continue with this process, using both the frequency distribution of the letters in the English language along with our knowledge of English words to help us, we can uncover the following plaintext:

WE WILL MEET IN THE MIDDLE OF THE
LIBRARY AT NOON ALL ARRANGEMENTS
ARE MADE

In practice, we might also look at the frequency distribution of letter pairs and even triples in addition to single letters.

Monoalphabetic Cipher Quiz

Monoalphabetic Cipher Quiz Solution

Vigenere Cipher

While a substitution cipher uses a single alphabet, a polyalphabetic cipher uses multiple substitution alphabets. The Vigenere cipher is the most well-known polyalphabetic cipher.

We can represent the Vigenere translation with the following matrix, M, whereby the ciphertext for a given plaintext P and key K resides at column P, row K in M.

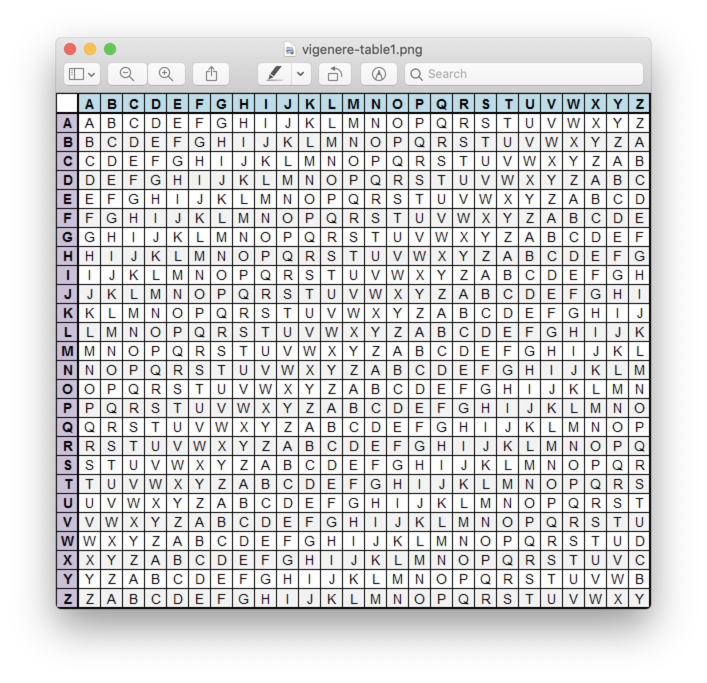
Suppose we want to encrypt the plaintext "ATTACKATDAWN" using the Vigenere cipher with "LEMON" as the key. Since Vigenere encryption proceeds characterwise, the key must be as long as the plaintext. We generate the keystream "LEMONLEMONLE" by repeating the key until the required number of characters are present.

To encrypt "A", we look at column "A" and row "L" of the matrix. The first character of the ciphertext is "L". To encrypt "T", we look at column "T" and row "E" of the matrix. The second character of the ciphertext is "X". To encrypt "T", we look at column "T" and row "M" of the matrix. The third character of the ciphertext is "F".

We can continue in this fashion to transform "ATTACKATDAWN" into "LXFOPVEFRNHR".

Vigenere Cipher Quiz

Vigenere Cipher Quiz Solution

What Should be Kept Secret?

While we should always keep our encryption keys a secret, our encryption algorithms should be public.

According to Kerckhoff's principle:

A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.

In general, we keep our encryption algorithms open so that they can be analyzed and improved by the broader community. More importantly, we don't have to rely on the secrecy of the algorithm for its security - the so-called "security by obscurity" principle. In practice, we should exclusively use the widely-known algorithms and standards.

Types of Cryptography

Secret key cryptography uses a single key for encryption and decryption, which means that the sender and the receiver must possess the same key.

Public-key cryptography uses two keys - a public and a private key - that are linked together mathematically. A user keeps their private key secret and announces their public key to other users.

The public key is used for encryption, and the private key is used for decryption. For example, Alice can use Bob's public key to encrypt a message that only Bob can decrypt because only Bob has the corresponding private key that can decrypt the message correctly.

The private key is also used for signing a message, and the public key can be used to verify the signature. For example, Alice can sign a message using her private key, and anyone knowing her public key can verify that only Alice can produce this signature.

Hash Functions

Hash functions are a third class of cryptographic functions. A hash function computes a fixed-length output - typically in the range of 128-512 bits - from a message of any size. This output is commonly referred to as a hash or message digest. Hash functions do not use keys.

We typically use hash functions for authentication and message authenticity/integrity. To provide these services, hash functions must satisfy the following properties.

Efficiency

A hash function should be able to compute a hash efficiently enough to make software and hardware implementations of the function practical.

One-way function

For a given hash function H and a given hash value v, finding the original message m, such that H(m) = v should be computationally infeasible.

Suppose Alice wants to authenticate herself to Bob. She can hash a secret S that she shares with Bob and send the hashed value to him. Bob can verify that Alice sent the message by hashing their shared secret himself and comparing it with the value he received.

Because Alice transmits the hash value over the Internet, we must assume that an attacker can intercept the message. If the hash function does not satisfy the one-way property, the attacker can reverse the function and recover S from its hash.

If the attacker knows S, they can impersonate Bob to Alice or Alice to Bob.

Weak collision resistance

Given a hash function H and a message m1, it should be computationally infeasible to find another message m2 such that H(m2) = H(m1).

This property is essential for message authenticity and integrity protection.

Suppose Alice sends a message M to Bob, and she wants to make sure Bob knows that she is the real author of M. Alice can do this by sending M along with a signed hash of M.

If the weak collision-resistant property is not present, an attacker may be able to craft a different message M', such that the hash of M' is the same as the hash of M.

If Bob receives M' and the original signed hash of M, Bob has no way of knowing that the message is not from Alice.

Strong collision-resistant

Given a hash function H, it should be computationally infeasible to find two messages m1 and m2 such that H(m2) = H(m1).

This property is stronger because it prevents an attacker from coming up with any two different messages that have the same hash value.

Suppose Alice owes Bob money. Bob can write an IOU message that Alice can hash and sign using her private key. If Bob can find two different messages that have the same hash value, one that requires Alice to pay a small amount, and another that requires her to pay a large amount, Bob may send Alice the message for the smaller amount and later claim that Alice owes him the larger amount.

Hash Functions for Passwords

The one-way property of hash functions - a hash function should be easy to compute, but impossible to invert - makes them a great candidate for password verification.

When a user authenticates themselves to a system, they often supply a password. The system hashes the supplied password and compares this hash against the saved hash of the password for that user. The system grants access if the two values match, denying access otherwise.

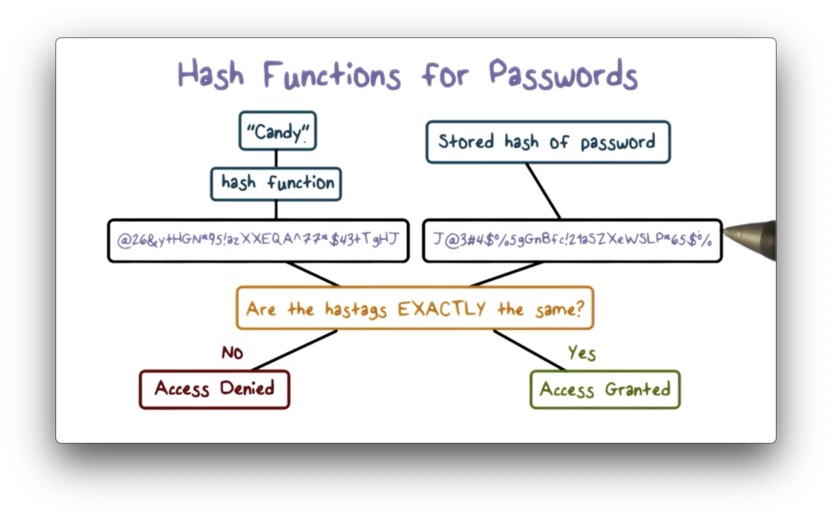
The advantage of this scheme is that the system only has to store the hashed passwords. If the system chose to store the cleartext passwords, then anyone who has access to the system can impersonate anyone else registered on the system after reading the password file.

If an attacker gains access to a system, they can steal the hashed passwords and compare the hashes against a dictionary of commonly-used passwords and their hashes to find matches. We must avoid using common passwords like "password" and "123456".

Hash Function Quiz

Hash Function Quiz Solution

The avalanche effect states that a small change in the input to a hash function causes a large change to the output. We want this in place as a way to obscure similar passwords. Without the avalanche effect, an attacker may be able to deduce password A from its hash value if he knows that the hash of a string B is similar to A's hash.

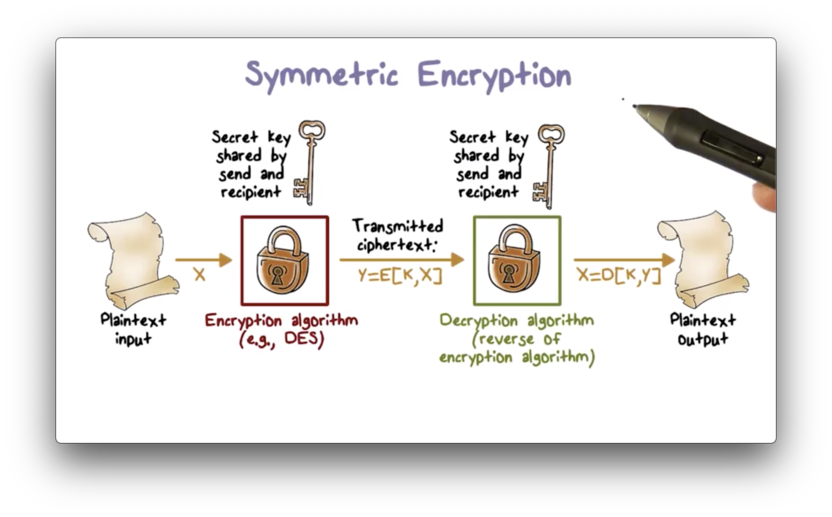
Symmetric Encryption

Symmetric encryption uses the same key for both encryption and decryption. The encryption algorithm takes the plaintext and the key as input and produces the ciphertext using substitution and permutation. The decryption algorithm reverses the encryption process, reproducing the original plaintext from the key and the ciphertext.

Comparison of Encryption Algorithms

The most important symmetric algorithms are the Data Encryption Standard (DES) block cipher and the Advanced Encryption Standard (AES) block cipher. A block cipher encrypts plaintext in fixed-size blocks and produces ciphertext blocks of equal size. DES and AES use different key sizes and block lengths.

Since a longer key indicates a larger keyspace, DES and AES can be distinguished by the amount of time necessary to successfully conduct a brute-force attack. The following table shows how much time is required to brute-force various ciphers with different key lengths.

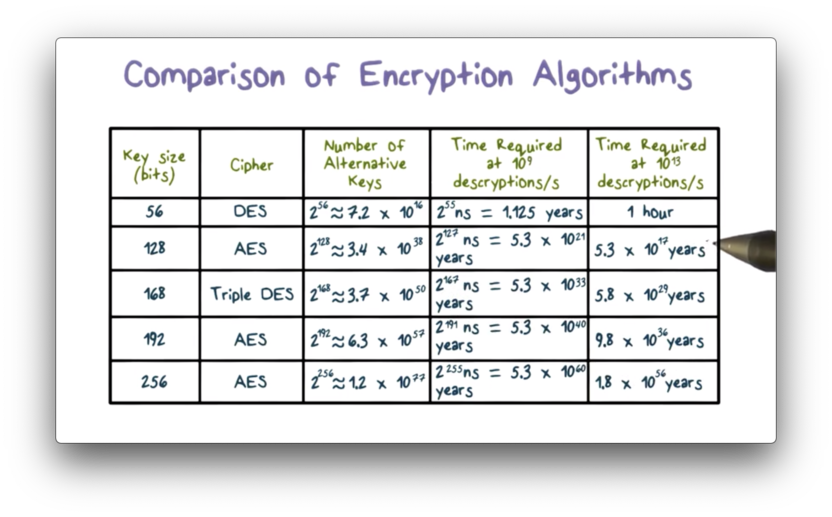
Note that DES - now seen as insecure - is breakable within an hour using a supercomputer. Ciphers with key lengths of 128 bits or greater are effectively unbreakable using modern processing power.

Symmetric Encryption Quiz

Symmetric Encryption Quiz Solution

Asymmetric Encryption

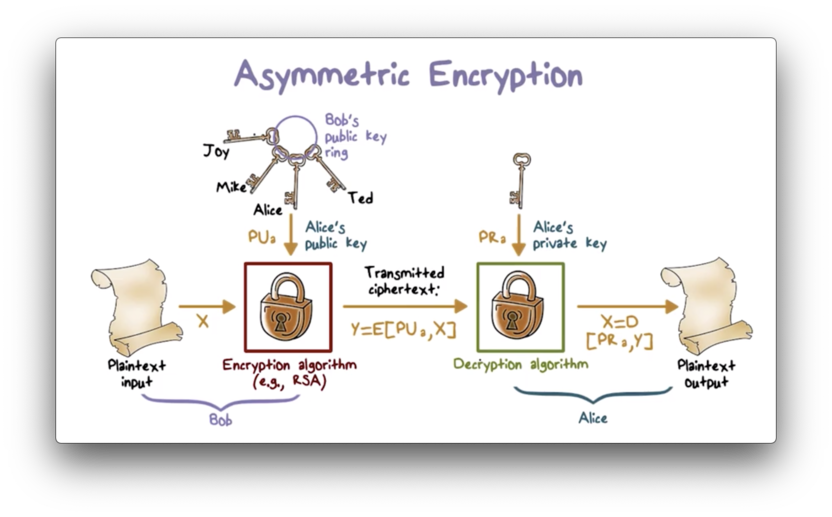
While symmetric encryption uses the same key for encryption and decryption, asymmetric encryption uses two keys: one for encryption and the other for decryption. The two keys are paired together mathematically such that if one key encrypts a message, only the other key can decrypt it.

To communicate using asymmetric encryption, a user must first generate a pair of keys. The public key can be sent to other users, while the private key must be known only to the user. A user might have a collection of public keys, one for each user with whom they communicate regularly.

If Bob wants to send a private message to Alice, Bob must first obtain Alice's public key. With Alice's public key in hand, Bob encrypts his message to Alice using an asymmetric encryption algorithm such as RSA. Bob then transmits the ciphertext to Alice, which she can decrypt using her private key.

Asymmetric Encryption Quiz

Asymmetric Encryption Quiz Solution

Digital Signatures

The public key in public-key encryption is genuinely public. Any user can broadcast their public key to the world for any other user to consume. Although this approach is very convenient, it has a significant weakness: any user can forge such a public announcement.

For example, an attacker can pretend to be Bob and send a public key to Alice. When she goes to send a message to the real Bob using the imposter's key, the attacker can intercept and decrypt the message. If Bob discovers that an attacker is forging his identity, he can send Alice his real public key, but a better solution to the problem is one that prevents the forgery in the first place.

Bob can prevent the forgery by obtaining a public key certificate from a certification authority (CA). Bob can contact the CA and provide them with his authentication information, such as his driver's license or his user id, as well as his public key.

The CA then constructs Bob's certificate using his identification, his public key, and some other information, such as the period of validity for the certificate. Finally, the CA hashes and signs this information with their private key and then appends this hash to the certificate.

Now Bob can send his public key certificate to Alice. When Alice receives the certificate, she can extract the key as well as the information about Bob and the certificate itself. Alice can then hash the certificate and use the CA's public key to decrypt the signed, appended hash. If the two hashes match, she can be sure that no one has tampered with the certificate.

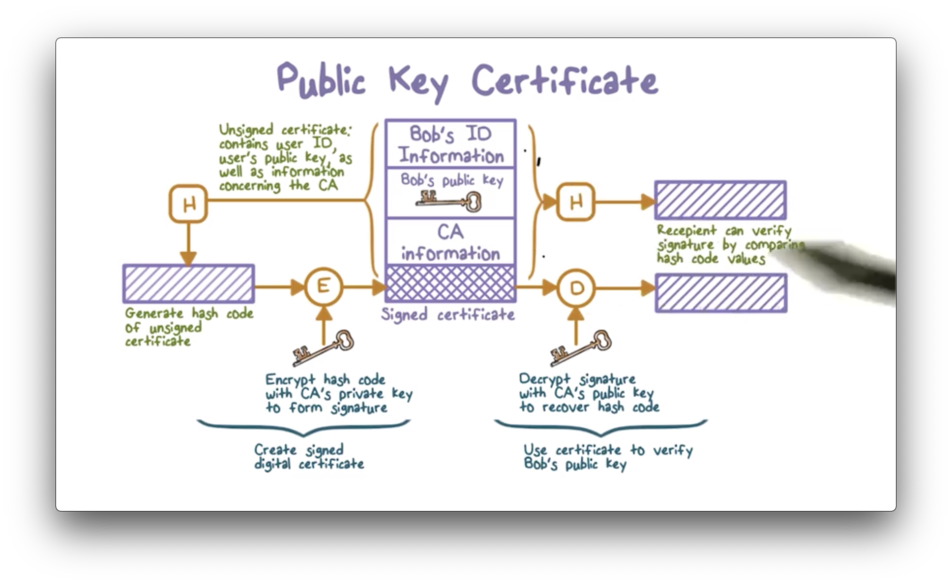
The underlying assumption is that the CA is a trusted party by everyone involved. In practice, the CA is a well-known company, such as VeriSign, Microsoft, Google, or Apple. Their public keys are already in your software - such as your browser - so they can automatically validate certificates that they have signed.

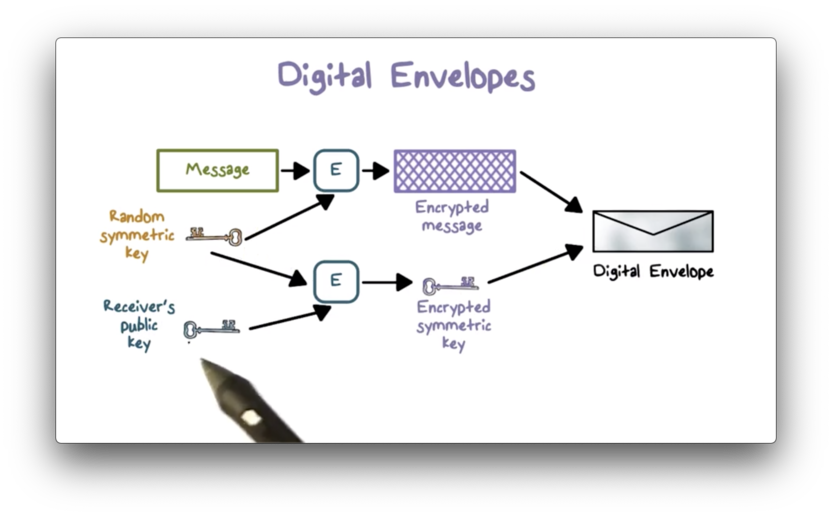
Digital Envelopes

Public-key encryption is typically used to establish a symmetric key, which is then used to encrypt subsequent communications amongst parties.

Suppose Alice and Bob wish to communicate securely.

Alice first creates a random symmetric key that she wants to share with Bob and encrypts her message to Bob using this key. She then encrypts the symmetric key with Bob's public key and transmits a digital envelope containing both the message and the encrypted key to Bob.

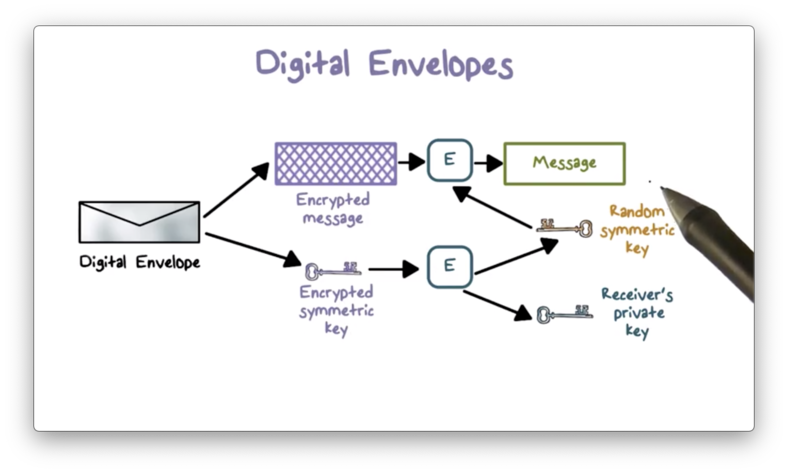
When Bob receives the envelope, he can use his private key to decrypt the encrypted symmetric key. With the decrypted key in hand, he can decrypt the actual message from Alice.

Encryption Quiz

Encryption Quiz Solution