Dyna

Overview

One problem with Q-learning is that it takes many experience tuples to converge. Gathering experience from the real world is expensive because it requires us to take real action - executing a live trade in our case - to gather information.

To address this problem, researchers developed a technique called Dyna. Dyna works by building models of the transition function, $T$, and reward function, $R$. Then, after each real interaction with the world, we hallucinate many additional interactions, typically a few hundred, which we use to update the Q-table.

Dyna-Q Big Picture

Dyna-Q is an algorithm developed by Richard Sutton intended to speed up learning, or policy convergence, for Q-learning. Remember that Q-learning is a model-free method, meaning that it does not rely on, or even know, the transition function, $T$, and the reward function, $R$. Dyna-Q augments traditional Q-learning by incorporating estimations of both $T$ and $R$, based on experience.

Let's quickly recap the Q-learning algorithm we've been using thus far. We first initialize our Q-table, and then we begin iterating. We observe a state, $s$, execute an action, $a$, after which we observe a new state, $s'$, and a reward, $r$. Using this experience tuple, we update our Q-table. Finally, we repeat the process, continuously gaining experience from the world and improving our Q-table.

When we augment Q-learning with Dyna-Q, we add three new pieces. First, we add logic that enables us to build models of $T$ and $R$. Then, for lack of a better term, we hallucinate a number of experiences. Finally, we update our Q-table according to the experience tuples we generated during the hallucination. We repeat these steps potentially several hundred times for each real experience.

When we talk about updating our model, what we want to do is find new values for $T$ and $R$. Remember that $T$ is the probability that if we are in state $s$ and take action $a$ we will end up in state $s'$, while $R$ is our expected reward from taking action $a$ in state $s$.

Before we talk about how we hallucinate an experience, it's essential to understand why we might want to do this in the first place. The issue is that interacting with the real world can be very expensive, in terms of time, money, or some other resource, while hallucinations are cheap. By hallucinating a large number of experiences - say 100 or 200 - for every real experience, we can amortize the cost of a real experience over many Q-table updates.

We can hallucinate an experience in two steps. First, we randomly select a state, $s$, and an action, $a$. Next, we infer the new state, $s'$, using $T$, and we infer the reward, $r$, using $R$. Using this synthetic experience tuple, we can update our Q-table.

Learning T

Remember that $T[s,a,s']$ represents the probability that if we are in state, $s$, and we take action, $a$, we end up in state, $s'$. To learn a model of $T$, we need to observe and record the frequency with which state transitions occur.

We can introduce a new table, $T_c$, of dimensions, $(S,A,S)$, where $S$ is the number of total possible states, and $A$ is the number of total possible actions. We initialize the cells in $T_c$ to a very small number to avoid a potential divide-by-zero situation.

As we iterate through the Q-learning process, we accumulate experience tuples. For each $s$, $a$, and $s'$ that we acquire, we increment the count in $T_c[s, a, s']$. In this fashion, we can record the frequency of state transitions, which serves as an empirical model of $T$.

How to Evaluate T Quiz

Assume we have been interacting with the real world for a while, and we would like to consult our model of $T$. Can you write an equation for $T$ in terms of $T_c$?

How to Evaluate T Quiz Solution

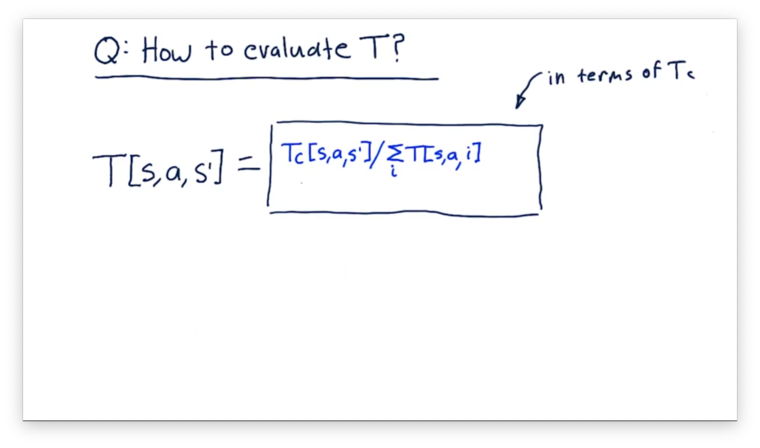
NOTE: The denominator in this equation should reference $T_c$, not $T$.

What we want to find here is the probability of a particular resulting state, $s'$, given a current state, $s$ and an action, $a$. Thus, we need a fraction where the numerator is the number of transitions from $s$ to $s'$, by way of $a$, and the denominator is the total number of transitions out of $s$, by way of $a$.

Let's consider the numerator first. The total number of transitions from $s$ to $s'$, as a result of $a$, is simply the recorded value, $T_c[s,a,s']$.

Next, let's consider the denominator. The total number of times we transitioned out of $s$ by taking $a$ is the sum $T_c[s,a,s_1] + T_c[s,a,s_2] + ... + T_c[s,a,s_n]$, where $n$ is the size of $S$, the state space.

Altogether, we have the following equation:

Learning R

In addition to learning a model of $T$, we also need to learn a model of $R$. Remember that $R[s,a]$ gives us the expected reward for taking an action, $a$, from a state, $s$. Recall also that each experience tuple contains an immediate reward, $r$, for taking the corresponding action from the corresponding state.

Given this, we can formulate a simple equation for $R$, which we update after each real experience. Notice that this update equation is very similar to the Q-table update equation, incorporating the same learning rate, $\alpha$, that we used in that equation.

Dyna-Q Recap