Machine Learning Trading
What Is a Company Worth
10 minute read
Notice a tyop typo? Please submit an issue or open a PR.
What Is a Company Worth
What Is a Company Worth Quiz
Suppose there is a company that consistently generates $1 per year. What is that company worth?

What Is a Company Worth Quiz Solution

Why Company Value Matters
In general, the fundamental value of a company increases monotonically over time, as seen by the following plot.
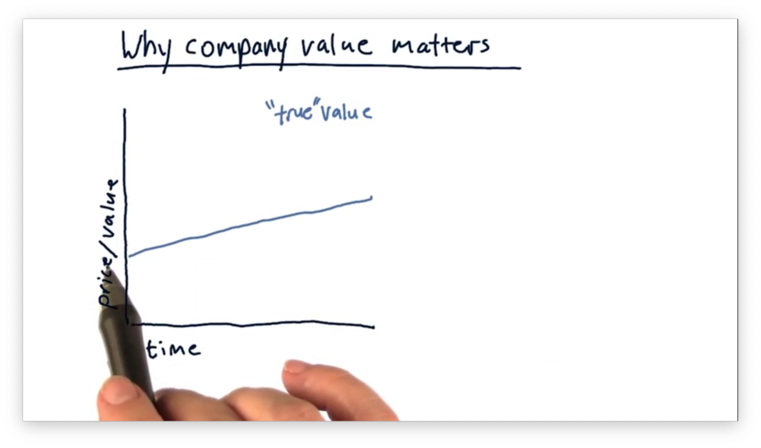
This fundamental value is distinct from the value as estimated by the market. In other words, what the stock market says a company is worth is often different than what a company is actually worth. On one particular day, the stock market might overvalue a company; on another, it might undervalue the company.
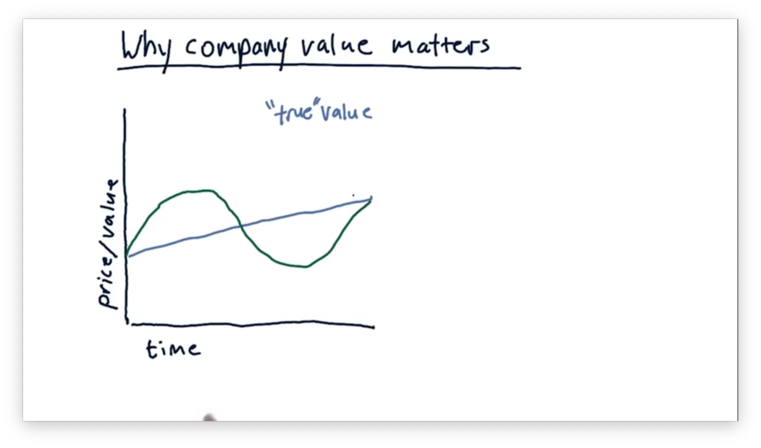
Many trading strategies focus on identifying where the current stock price diverges from the true value of the company. For example, if we see a stock price that surpasses this value, we know to sell the stock. Conversely, a stock price that falls below this value signals that we should buy the stock.
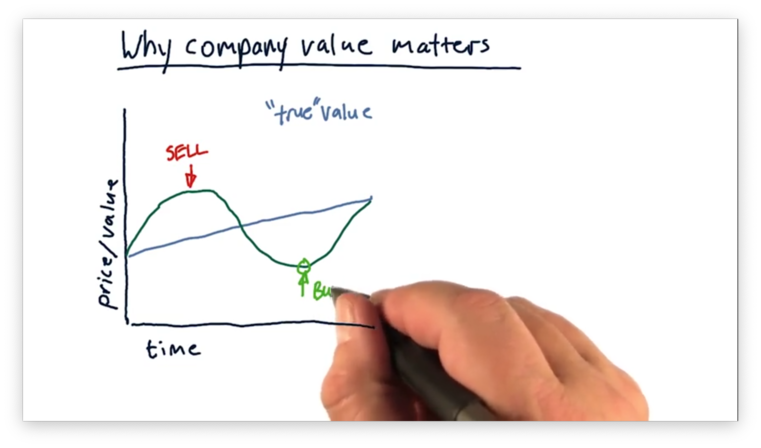
There are many different ways we can estimate the true value of a company, such as intrinsic value, book value, and market capitalization.
Intrinsic value bases the value of the company on future dividends. A dividend is a cash payment, often a few dollars per share, that companies award to shareholders on a quarterly or yearly basis. Intrinsic value accumulates all of the future dividends across all shares of stock to provide a valuation for a company.
Book value determines how much a company is worth by looking at the value of the assets that the company owns. In other words, if the company were to sell everything - factories, inventory, investments, and so on - the amount of money they would receive in the sale would be their book value.
Finally, market capitalization calculates company value as the product of the number of outstanding shares in the market and the current share price. For example, if Apple has 1,000,000 outstanding shares, priced at $1,000 per share, its value, based on market cap, would be $1 billion.
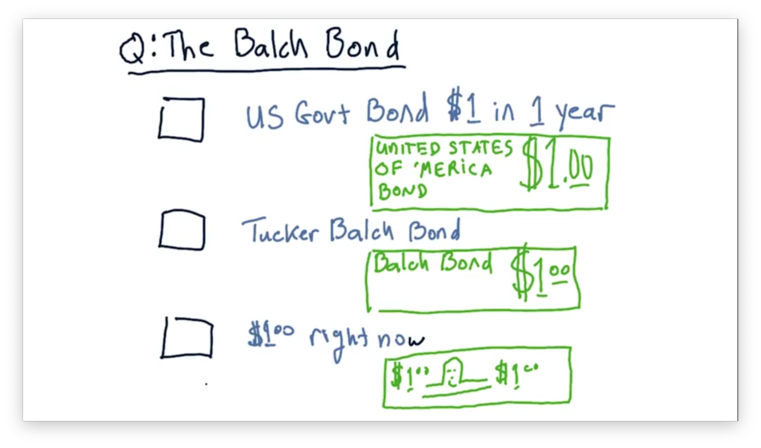
The Balch Bond Quiz
Assume that we are in a position to receive one of three different assets.
The first asset is a $1 bill: cold, hard cash. The second asset is a Tucker Balch bond; essentially, a promise certified by the professor that he will pay us $1 in one year. The third asset is a US Government bond, which also pays out $1 in one year, but is backed by the United States government.
Which of these assets would you rather receive? Rank the choices from 1 (best) to 3 (worst).
The Balch Bond Quiz Solution
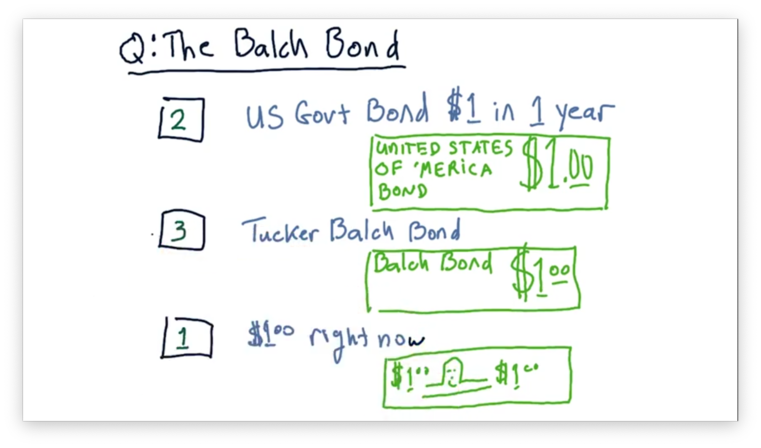
The most valuable asset among these three is the $1 delivered right now because you can spend it right now. The other two are promises for a reward at some point in the future. Among these two bonds, the one backed by the US government is likely more valuable than the one backed by the professor.
The Value of a Future Dollar
As we just saw, a dollar delivered today is more valuable than the promise of a dollar delivered at some point in the future. Additionally, we agreed that the promise of a future dollar is worth more when backed by the US government than when backed by Professor Balch.
We need to account for two factors when thinking about the value of a promised dollar: who is making the promise and how long we have to wait for them to deliver the dollar.
Formally, we are trying to find the present value of a dollar delivered in the future as a fraction of its future value . Keep in mind that the future value is nothing more than the value that we are promised; for this example, the future value of a promise of $1 is $1.
Given an interest rate, and a waiting period, , measured in years, we can calculate as follows.
Let's first consider the case of receiving a one-dollar bill right now. Since we don't have to wait, and . In other words, the payment is fulfilled immediately and is worth the face value of the bill: $1.
Let's look at a different example. Suppose that the United States government offers a bond at a 1% interest rate. The present value of $1, paid to us in one year, at a 1% interest rate is
In other words, we should only buy this government bond if we have to pay $0.99 or less.
Now consider the Tucker Balch Bond. Professor Balch can't sell us his bond with the same interest rate as the government bond; since he is less trustworthy than the US government, a smart investor would pick the government bond every time.
Professor Balch can only attract investors by offering a higher interest rate, such as 5%. The present value of $1, paid to us in one year, at a 5% interest rate is
In other words, if Professor Balch wants to attract us to buy his $1 bond, he could only charge us $0.95.
We can plot the present value of a $1 bond backed by both the US government and Tucker Balch, as a function of .
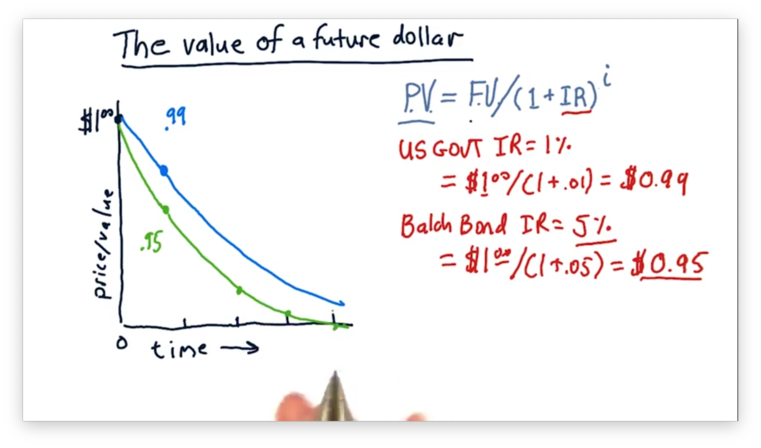
Here we see two curves demonstrating exponential decay. As our above calculations have confirmed, the present value of the less trustworthy bond, with the higher interest rate, is always worth less than the present value of the more trustworthy bond, with the lower interest rate, for any value of .
Intrinsic Value
Intrinsic value uses dividends to measure the value of a company. Remember that dividends are cash payments awarded to shareholders on a quarterly or yearly basis.
In some respect, then, dividends are similar to the bonds we described above in that they are a promise of a future payment. We can examine the present value of a single dividend in just the same way we computed the present value of a single bond.
We can also compute the present intrinsic value, , of the whole company by taking the sum of the present values of all dividends to be distributed.
While a bond issuer states the interest rate, , that a bond buyer is going to receive, the process works differently regarding dividends. Instead of interest rate, we consider the discount rate, which is a measure of how risky we think an investment in a company might be.
For example, we might think that investing in Apple is very safe, as safe, in fact, as purchasing a US government bond. In this case, we would set the discount rate equal to the US bond rate for Apple.
However, if we are less sure that a company can fulfill its promise to deliver dividends, we need to increase the discount rate. By increasing the discount rate, we imply that we expect a higher future payment in exchange for a somewhat riskier upfront investment.
Given a discount rate, , we can compute as follows.
This infinite sum reduces to a simple expression.
Let's consider a company that generates a $1 dividend. Suppose that, after much research, we decide that the risk level of an investment in this company is such that we deserve future dividends at a 5% discount rate.
The present value of this company is
Intrinsic Value Quiz
Consider a company that pays a dividend of $2 per year. Given a discount rate of 4%, what is the intrinsic value of this company?

Intrinsic Value Quiz Solution

The present value, , of a company is equal to the future value, , divided by the discount rate, . Given and ,
Book Value
A classic definition of book value is total assets minus intangible assets and liabilities.
Tangible assets are those that are easy to price: factories, offices, inventory, and so on. Intangible assets, like patents, or the value of a brand, are much harder to price. Liabilities refer to things that are owed, like loans, debts, or other obligations.
Let's consider a company that owns four factories, each priced at $10 million, and three patents, each valued at $5 million. Additionally, suppose the company has one liability, a loan worth $10 million.
If we take the total value of the assets, $55 million, and subtract the intangible assets, $15 million in patents, and the $10 million liability, we get a book value of $30 million for this company.
Market Capitalization
Alternatively, we can let the market determine the value of a company. Market capitalization is the product of the number of outstanding shares and the share price. For instance, a company with 1,000,000 shares and a share price of $100 has a market capitalization of $100,000,000.
Why Information Affects Stock Price
If you follow the stock market, you may have noticed that when news comes out about a particular company, that company's stock price may change considerably.
The reason for this is that buying and selling stock is the primary mechanism by which investors voice their support, or lack thereof, for a particular company. If they think that a company is overvalued, they are going to sell, and the stock price is going to drop. Conversely, if they think that a company is undervalued, they are going to buy, and the stock price is going to increase.
As an example, let's consider an island company whose business is to grow and sell coconuts. Suppose news comes out that the CEO of this company is ill. Perhaps he has cancer or some other disease that prevents him from effectively collecting coconuts.
Certainly, this news should drive the stock price downward. The health of the CEO affects the health of the company, which reduces either the size of our dividends, or the likelihood that we will receive them, or both. As a result, the intrinsic value of the company decreases sharply.
Let's consider a different piece of news. Recent reports are showing that the soil on the island is contaminated. This type of news is known as sector news; in other words, it affects all of the companies in the business sector of growing coconuts on this island.
Let's consider a final piece of news. New data comes out demonstrating the sea-level is rising. This type of news is known as market-wide news as it affects all companies on all islands.
Any of these stories may reduce an investor's belief in the ability of the coconut company to provide future dividends. This reduction might lead such an investor to sell off their stock, thus driving down the share price.
Compute Company Value Quiz
Consider a fictitious airline company.
This company owns 10 airplanes, each valued at $10 million. Additionally, it has a brand name worth another $10 million. Finally, it has an outstanding loan for $20 million. What is the book value of this company?
This company pays $1 million per year in dividends. Assuming a 5% discount rate, what is the intrinsic value of this company?
This company has one million shares of stock outstanding. Given a stock price of $75 per share, what is the market capitalization of this company?

Compute Company Value Quiz Solution

To calculate book value, we take the value of the total assets and subtract the intangible assets, like the brand, and the liabilities. Given $110,000,000 in total assets, a $10,000,000 intangible asset, and a $20,000,000 liability, the book value for this company is $80,000,000.
To compute the intrinsic value, we divide the value of the dividends, $1,000,000, by the discount rate, 0.05, to get $20,000,000.
To compute the market capitalization, we take the product of the share price, $75, and the number of outstanding shares, 1,000,000, to get $75,000,000.
Would you Buy this Stock Quiz
Since this company has a market capitalization of $75,000,000, we could buy all of the shares and, effectively the company, for $75,000,000. Should we?

Would you Buy this Stock Quiz Solution

It might seem like a tricky question, given such a relatively low intrinsic value, but it's not. We should buy this company for $75,000,000 and then break it apart and sell the individual assets for $80,000,000 to get an immediate $5,000,000 profit.
Stock prices very rarely dip below book value for this exact reason; otherwise, predatory buyers swoop in and buy the whole company just to sell it for parts.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy