Machine Learning Trading
Ensemble Learners, Bagging, and Boosting
4 minute read
Notice a tyop typo? Please submit an issue or open a PR.
Ensemble Learners, Bagging, and Boosting
Ensemble Learners
So far, we've looked at using a single type of learning method to build a single model. For example, we might build a KNN model from our training data, and then query it with new observations to get new predictions.
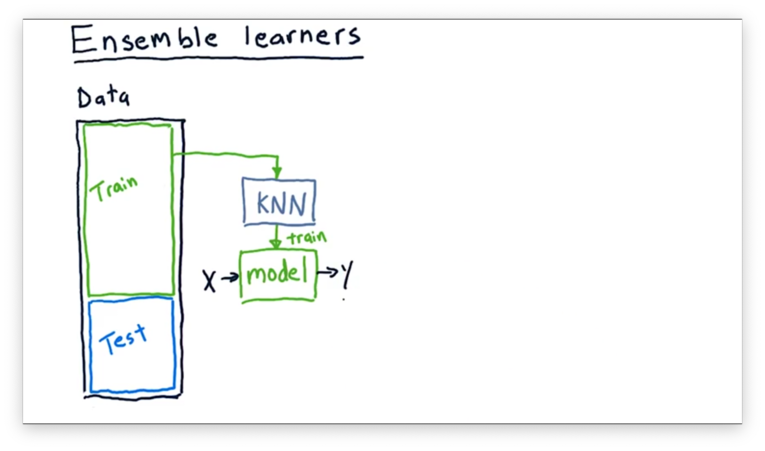
Nothing is restricting us to this one-model paradigm. We can build an ensemble of learners and combine the outputs of their models to provide a composite prediction.
For example, we might have a KNN learner, a linear regression learner, a decision tree learner, and an SVM-based learner. Each learner in the ensemble is trained using the same data, and we query the ensemble by querying each model and combining the results.
For classification problems, the composite prediction might be the mode of the individual predictions; in other words, each model votes, and the highest vote wins. For regression problems, we typically take the mean of the individual outputs.
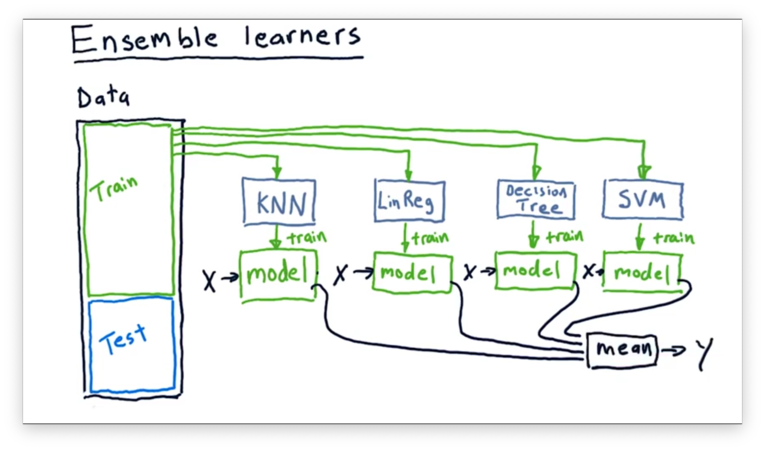
We use ensembles for two reasons: first, they often have lower error than any individual learner might have by itself, and, second, ensemble learners are less likely to overfit than a single learner.
We can offer an intuitive explanation for these claims. Every model that we might use has its own type of bias. For example, a linear regression learner is biased in its assumption that the relationship between and is linear. When we combine learners, these individual biases can cancel each other out, to an extent.
How to Build an Ensemble Quiz
How might we go about building an ensemble of learners?

How to Build an Ensemble Quiz Solution

We can create an ensemble by training several parameterized polynomials of differing degrees (A) or by training several KNN models using different subsets of data (B).
It doesn't make sense to train KNN models using randomized -values, because we want to train any model we plan to use on the actual data in our training set. As a result, neither (C) nor (E) is correct.
Instead of using just polynomial learners or KNN learners, we can combine the two into a super ensemble (D) for even better results.
Bootstrap Aggregating: Bagging
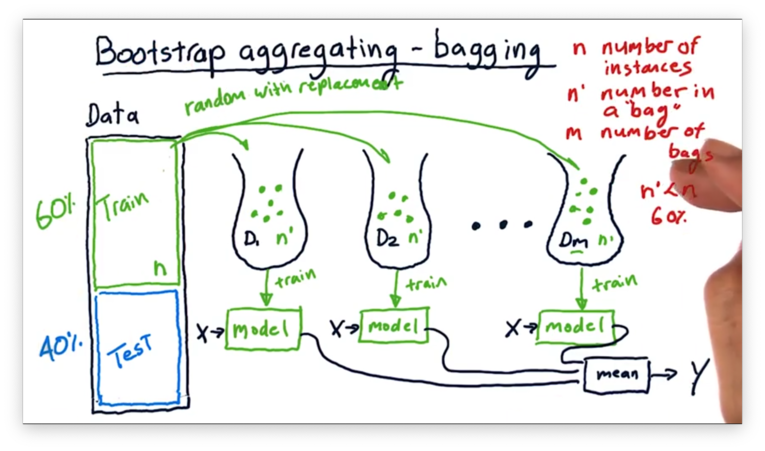
Instead of building an ensemble using different types of learners, we can use multiple instances of the same learner, training each on a slightly different subset of the data. This process is called bootstrap aggregating, or bagging.
From the original set of training data, containing examples, we can create bags of examples by sampling the training data randomly, with replacement, times.
We then take each bag and use it to train an instance of our learner. Just like when we have an ensemble of different learning algorithms, we can query our bagged ensemble in the same way. We pass the same to each trained model and collect and average the results to generate a .
Overfitting Quiz
Which of these two models is least likely to overfit?
Aside: the screenshot says "most likely to overfit", but he selects the model that is least likely to overfit.

Overfitting Quiz Solution

Bagging Example
Suppose we have the following data, and we'd like to create several 1-nearest neighbor models to describe this data.
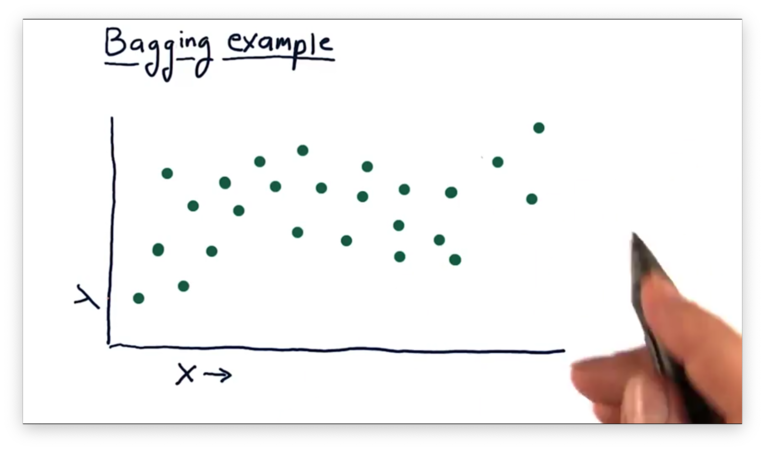
First, we randomly select the data points, circled below, for our first training bag.
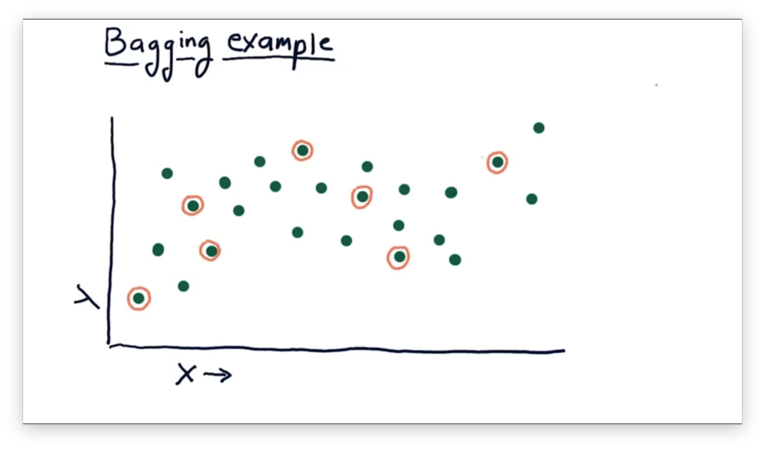
From these points, we can generate the following model.
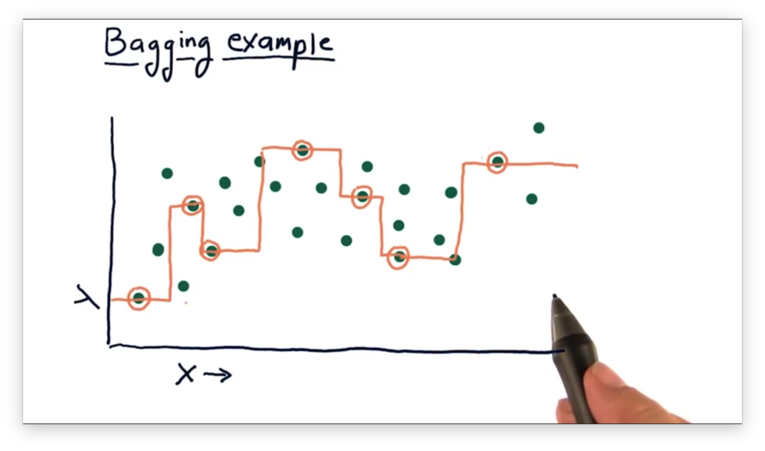
We can generate another model by selecting another random subset of data points.
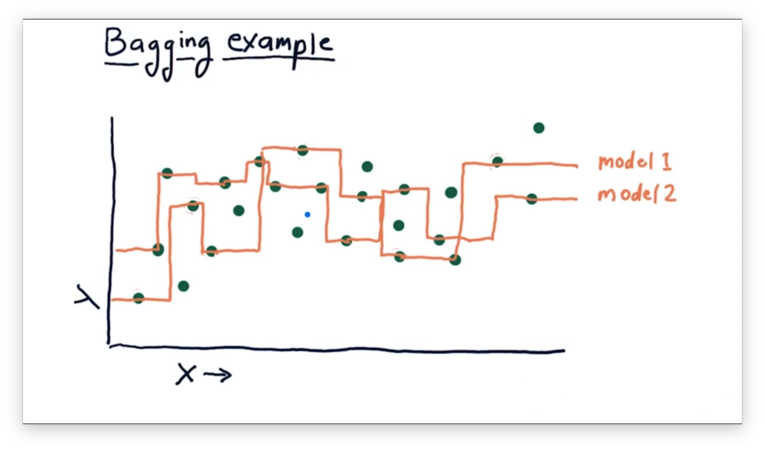
While both of these models, taken alone, look woefully overfit, we can create an ensemble that averages their predictions for each query.
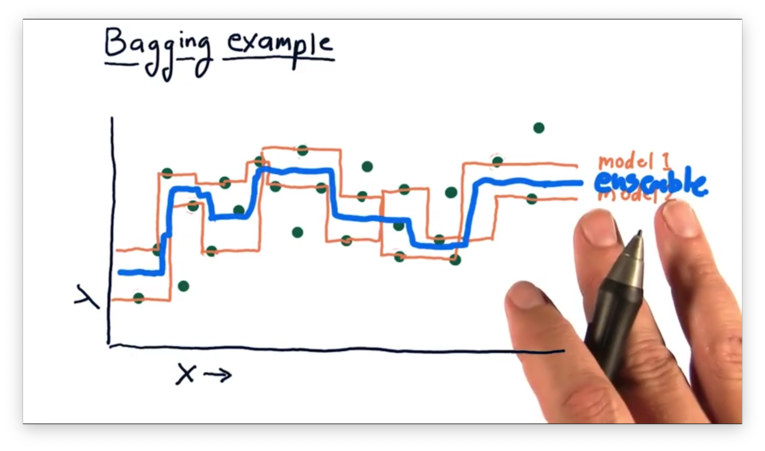
Indeed, the ensemble model is "smoother" than either of the constituent models. We don't have to stop at just two learners; instead, we can create an even larger ensemble.
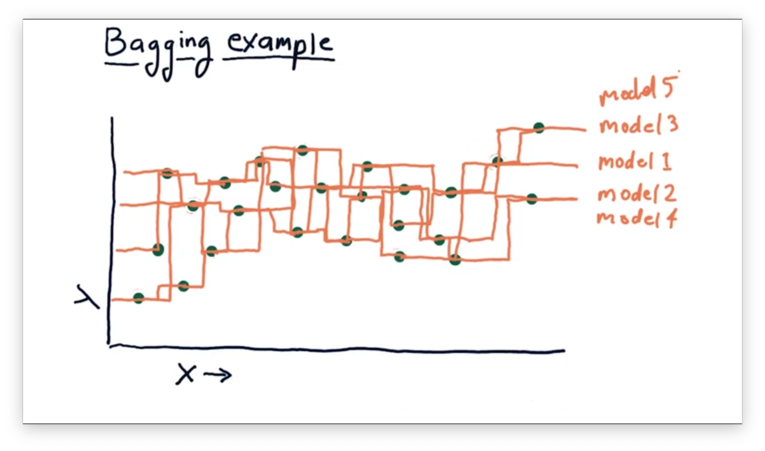
If we plot the ensemble created from these five learners, we see an even smoother model than the one generated by the previous ensemble.
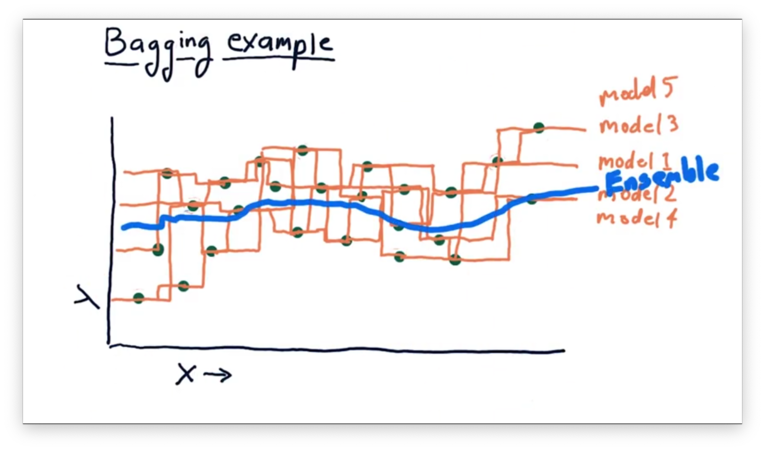
Boosting
Boosting is a relatively simple variation on bagging that strives to iteratively improve the ensemble by focusing on areas in which it is currently performing poorly. One of the most well-known boosting algorithms is Adaptive Boosting (AdaBoost).
Using AdaBoost, we build our first bag of data in the usual way: random selection, with replacement, from our training data. We then train a model on this bag.
Next, we test the model using the entire set of training data. During this test, we are going to discover that our model has a larger prediction error for some data points and not others.
When we go to build our next bag of data, we no longer select our examples randomly from the training set. Instead, we weight the probability of selection as a function of the prediction error, so that poorly predicted examples are more likely to be chosen.
In other words, we bump the worst-predicted examples to the front of the line so that the next model we train can fix the errors of the first.
We build a model from our second bag and then test both models, as an ensemble, over the entire training set. We again adjust the probabilities of selecting training examples for our next bag according to the prediction errors that the ensemble generates. We continue this refinement until we have bags.
Overfitation Quiz
As we increase the number of models in our ensemble, which of the following strategies is more likely to overfit?

Overfitation Quiz Solution

AdaBoost focuses primarily on improving the system for specific data points; in other words, it strives to fit. As a result, it is more susceptible to overfitting than is simple bagging.
OMSCS Notes is made with in NYC by Matt Schlenker.
Copyright © 2019-2023. All rights reserved.
privacy policy